题目内容
16.将双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点、右顶点、虚轴的一个端点所组成的三角形叫做双曲线的“黄金三角形”,则双曲线C:x2-y2=4的“黄金三角形”的面积是( )| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
分析 根据条件求出右焦点、右顶点、虚轴的一个端点的坐标,结合三角形的面积公式进行计算即可.
解答 解:由x2-y2=4得$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{4}$=1,
则a2=b2=4,则a=2,b=2,c=2$\sqrt{2}$,
则双曲线的右焦点、右顶点、虚轴的一个端点的坐标分别为(2$\sqrt{2}$,0),(2,0),(0,2),
故所求“黄金三角形”的面积S=$\frac{1}{2}$(2$\sqrt{2}$-2)×2=2$\sqrt{2}$-2,
故选:B
点评 本题主要考查双曲线的性质,根据定义求出交点坐标是解决本题的关键.

练习册系列答案
相关题目
7.已知动圆过定点A(3,0),且与圆(x+3)2+y2=64相切,则动圆的圆心P的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
4.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{1}{2}$x,则双曲线的离心率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{5}}{2}$ |
11.设全集U=R,集合A={x|x2>1},B={x|x>2},则A∩(∁UB)=( )
| A. | {x|-1≤x<2} | B. | {x|x<-1或1<x≤2} | C. | {x|x<-1} | D. | {x|x>2} |
1.已知正数组成的等比数列{an},若a2•a19=100,那么a8+a13的最小值为( )
| A. | 20 | B. | 25 | C. | 50 | D. | 不存在 |
8.如图,给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$+$\frac{1}{101}$的值的一个程序框图,判断框内应填入的条件是( )

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
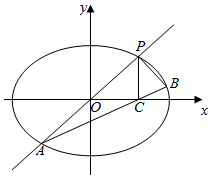 已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.
已知椭圆w:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,$\sqrt{2}$),椭圆w上任意一点到两焦点的距离之和为4.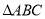 中,
中,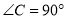 ,点
,点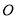 在
在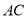 上,以
上,以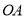 为半径的
为半径的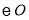 交
交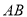 于点
于点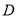 ,
,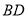 的垂直平分线交
的垂直平分线交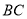 于点
于点 ,交
,交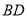 于点
于点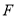 ,连接
,连接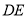 .
.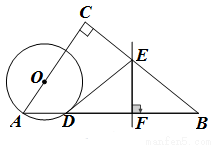
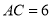 ,
,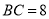 ,
, ,求线段
,求线段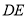 的长.
的长.