题目内容
11.设全集U=R,集合A={x|x2>1},B={x|x>2},则A∩(∁UB)=( )| A. | {x|-1≤x<2} | B. | {x|x<-1或1<x≤2} | C. | {x|x<-1} | D. | {x|x>2} |
分析 求出A中不等式的解集确定出A,找出A与B补集的交集即可.
解答 解:∵全集U=R,B={x|x>2},
∴∁UB={x|x≤2},
又A={x|x>1或x<-1},
∴A∩(∁UB)={x|x<-1或1<x≤2},
故选:B.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.2015年秋季开始,本市初一学生开始进行开放性科学实践活动,学生可以在全市范围内进行自主选课类型活动,选课数目、选课课程不限.为了了解学生的选课情况,某区有关部门随机抽取本区600名初一学生,统计了他们对于五类课程的选课情况,用“+”表示选,“-”表示不选.结果如表所示:
(1)估计学生既选了课程三,又选了课程四的概率;
(2)估计学生在五项课程中,选了三项课程的概率;
(3)如果这个区的某学生已经选了课程二,那么其余四项课程中他选择哪一项的可能性最大?
| 人数 课程 | 课程一 | 课程二 | 课程三 | 课程四 | 课程五 |
| 50 | + | + | - | + | - |
| 80 | + | + | - | - | - |
| 125 | + | - | + | - | + |
| 150 | - | + | + | + | - |
| 94 | + | - | - | + | + |
| 76 | - | - | + | + | - |
| 25 | - | - | + | - | + |
(2)估计学生在五项课程中,选了三项课程的概率;
(3)如果这个区的某学生已经选了课程二,那么其余四项课程中他选择哪一项的可能性最大?
6.某单位从包括甲、乙在内的5名应聘者中招聘2人,如果这5名应聘者被录用的机会均等,则甲、乙两人中至少有1人被录用的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{7}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
16.将双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点、右顶点、虚轴的一个端点所组成的三角形叫做双曲线的“黄金三角形”,则双曲线C:x2-y2=4的“黄金三角形”的面积是( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
3.已知0<θ<$\frac{π}{2}$,f(θ)=1+m+m($\frac{cosθ-1}{sinθ}$)+$\frac{sinθ-1}{cosθ}$(m>0),则使得f(θ)有最大值时的m的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
20.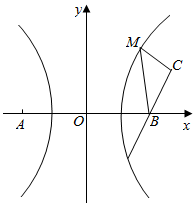 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
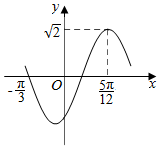 曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).
曲线f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,曲线f(x)的解析式为f(x)=$\sqrt{2}$sin(2x-$\frac{π}{3}$).