题目内容
1.已知正数组成的等比数列{an},若a2•a19=100,那么a8+a13的最小值为( )| A. | 20 | B. | 25 | C. | 50 | D. | 不存在 |
分析 由正数组成的等比数列{an},可得a2•a19=100=a8a13,利用基本不等式的性质即可得出.
解答 解:正数组成的等比数列{an},∵a2•a19=100,∴a2•a19=100=a8a13,
∴a8+a13≥2$\sqrt{{a}_{8}{a}_{13}}$=20,当且仅当a8=a13=10时,a8+a13的最小值为20,
故选:A.
点评 本题考查了等比数列的性质、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元,销售单价与日均销售量的关系如下表所示.
请根据以上数据分析,这个经营部定价在11.5元/桶才能获得最大利润.
| 销售单价/元 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 日均销售量/桶 | 480 | 440 | 400 | 360 | 320 | 280 | 240 |
13.已知(1-2x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a3+a4等于( )
| A. | 0 | B. | -240 | C. | -480 | D. | 960 |
16.将双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1的右焦点、右顶点、虚轴的一个端点所组成的三角形叫做双曲线的“黄金三角形”,则双曲线C:x2-y2=4的“黄金三角形”的面积是( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 1 | D. | 2 |
13.各项均为正数的等差数列{an}中,2a6+2a8=a72,则a7=( )
| A. | 2 | B. | 4 | C. | 16 | D. | 0 |
9.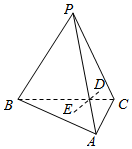 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )| A. | DE∥PB | B. | 当AB=BC且PA=AC时DE∥PB | ||
| C. | 当且仅当AB=BC且PA=AC时,DE⊥AC | D. | DE⊥AC |
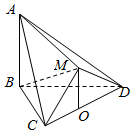 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM.
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,∠CMD=90°,平面CMD⊥平面BCD,AB⊥平面BCD,点O为CD的中点,连接OM. 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.