题目内容
8.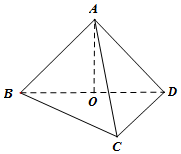 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,求(1)AC与平面BCD所成角的大小;
(2)二面角A-BC-D的大小.
分析 (1)由已知得BD=$\sqrt{3}$,OB=OC=OD=$\frac{\sqrt{3}}{2}$,AO⊥平面BCD,AC与平面BCD所成角为∠ACO,由此能求出AC与平面BCD所成角的大小为30°.
(2)由已知得AO=$\frac{1}{2}$,AB=AC=1=BC,取BC中点E,则∠AEO是二面角A-BC-D的平面角,由此能求出二面角A-BC-D的正切值.
解答 解:(1)如图,∵Rt△BCD中,BC=1,CD=$\sqrt{2}$,
∴BD=$\sqrt{1+2}=\sqrt{3}$,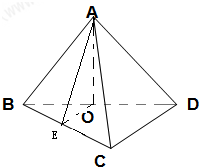
∵O是Rt△BCD斜边中点,∴OB=OC=OD=$\frac{\sqrt{3}}{2}$,
∵A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,
∴AO⊥平面BCD,
∴AC与平面BCD所成角为∠ACO,
∵cos=$\frac{CO}{AC}=\frac{\sqrt{3}}{2}$,∴∠ACO=30°,
∴AC与平面BCD所成角的大小为30°.
(2)由(1)得AO=$\frac{1}{2}$,AB=AC=1=BC,∴△ABC是正三角形
取BC中点E,则AE⊥BC,OE⊥BC,
AE=$\frac{\sqrt{3}}{2}$,OE=$\frac{1}{2}$DC=$\frac{\sqrt{2}}{2}$,
则∠AEO是二面角A-BC-D的平面角,tan∠AEO=$\frac{\sqrt{2}}{2}$.
∴二面角A-BC-D的大小为arctan$\frac{\sqrt{2}}{2}$.
点评 本题考查直线与平面所成角的大小的求法,考查二面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.函数y=x2-2x的递减区间为( )
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
20.在△ABC中,D是边AB上的中点,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{c}$,则向量$\overrightarrow{CD}$=( )
| A. | -$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{c}$ | C. | -$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$ |
17.已知△ABC的边BC上有一点D满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,则$\overrightarrow{AD}$可表示为( )
| A. | $\overrightarrow{AD}$=-2$\overrightarrow{AB}$+3$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |