题目内容
16.函数y=x2-2x的递减区间为( )| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | (0,+∞) |
分析 根据所给的二次函数的二次项系数大于零,得到二次函数的图象是一个开口向上的抛物线,根据对称轴,考查二次函数的变化区间,得到结果.
解答 解:∵函数y=x2-2x的二次项的系数大于零,
∴抛物线的开口向上,
∵二次函数的对称轴是x=1,
∴函数的单调递减区间是(-∞,1).
故选A.
点评 本题考查二次函数的性质,考查二次函数的最基本的运算,是一个基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
6.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥PF2,则以F1,F2为焦点且经过P的椭圆的离心率等于( )
| A. | .$\frac{{\sqrt{5}}}{5}$ | B. | .$\frac{{\sqrt{6}}}{3}$ | C. | .$\frac{{\sqrt{2}}}{2}$ | D. | .$\frac{1}{2}$ |
11.双曲线$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{3+m}$=1的一个焦点为(2,0),则m的值为( )
| A. | $\frac{1}{2}$ | B. | 1或3 | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
1.等差数列{an}的前n项和为Sn,且$\frac{{S}_{6}}{{S}_{3}}$=4,则$\frac{{S}_{5}}{{S}_{6}}$=( )
| A. | $\frac{9}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{25}{36}$ | D. | 4 |
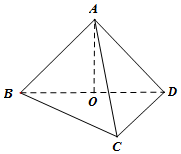 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
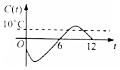
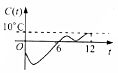
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$, 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )