题目内容
13.已知:$0<α<\frac{π}{2}<β<π,cos(β-\frac{π}{4})=\frac{1}{3}$,$sin(α+β)=\frac{4}{5}$.(1)求sin2β的值;
(2)设函数f(x)=cosx-sinx,试求 f(α)的值.
分析 (1)【解法一】利用二倍角与同角的三角函数关系求出cos(2β-$\frac{π}{2}$),即sin2β的值;
【解法二】利用两角差的余弦公式得出$cosβ+sinβ=\frac{{\sqrt{2}}}{3}$,再两边平方求出sin2β的值;
(2)根据α、β的取值范围,利用同角的三角函数关系和三角恒等变换,求f(α)的值即可.
解答 解:(1)【解法一】∵cos(β-$\frac{π}{4}$)=$\frac{1}{3}$,
∴cos(2β-$\frac{π}{2}$)=2cos2(β-$\frac{π}{4}$)-1=2×$\frac{1}{9}$-1=-$\frac{7}{9}$,----(3分)
即sin2β=-$\frac{7}{9}$;-------(6分)
【解法二】∵cos(β-$\frac{π}{4}$)=$\frac{1}{3}$,
∴$\frac{{\sqrt{2}}}{2}•(cosβ+sinβ)=\frac{1}{3}$,
即$cosβ+sinβ=\frac{{\sqrt{2}}}{3}$;------(3分)
两边平方得:$1+sin2β=\frac{2}{9}$,
即sin2β=-$\frac{7}{9}$;------(6分)
(2)∵0<α<$\frac{π}{2}$<β<π,
∴$\frac{π}{4}$<β-$\frac{π}{4}$<$\frac{3π}{4}$,$\frac{π}{2}$<α+β<$\frac{3π}{2}$,
∴sin(β-$\frac{π}{4}$)>0,cos(α+β)<0,
∴sin(β-$\frac{π}{4}$)=$\frac{2\sqrt{2}}{3}$,----------(8分)
cos(α+β)=-$\frac{3}{5}$;-----------(10分)
∴f(α)=cosα-sinα
=$\sqrt{2}$cos(α+$\frac{π}{4}$)
=$\sqrt{2}$cos[(α+β)-(β-$\frac{π}{4}$)]
=$\sqrt{2}$[cos(α+β)cos(β-$\frac{π}{4}$)+sin(α+β)sin(β-$\frac{π}{4}$)]
=$\sqrt{2}$(-$\frac{3}{5}$×$\frac{1}{3}$+$\frac{4}{5}$×$\frac{2\sqrt{2}}{3}$)
=$\frac{16-3\sqrt{2}}{15}$.--------(12分)
点评 本题考查了三角函数的求值问题,也考查了三角恒等变换应用问题,是中档题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | -17 | B. | -15 | C. | -6 | D. | 0 |
| A. | $\frac{9}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{25}{36}$ | D. | 4 |
| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |
| x | 1 | 2 | 3 | 4 | 5 |
| lnx | 0 | 0.69 | 1.10 | 1.39 | 1.61 |
| x-2 | -1 | 0 | 1 | 2 | 3 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
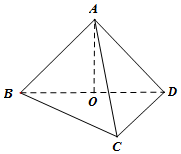 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,