题目内容
17.已知△ABC的边BC上有一点D满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,则$\overrightarrow{AD}$可表示为( )| A. | $\overrightarrow{AD}$=-2$\overrightarrow{AB}$+3$\overrightarrow{AC}$ | B. | $\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$ | C. | $\overrightarrow{AD}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$ | D. | $\overrightarrow{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AC}$ |
分析 根据向量的三角形法则和向量的几何意义即可求出.
解答 解:由$\overrightarrow{BD}$=3$\overrightarrow{DC}$,
则$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{BC}$=$\overrightarrow{AB}$+$\frac{1}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$,
故选:B
点评 本题考查了向量的三角形法则和向量的几何意义,属于基础题.

练习册系列答案
相关题目
2.在△ABC中,角A,B,C所对应的边长分别为a,b,c,面积为S,若S+a2=(b+c)2,则tanA=( )
| A. | $\frac{8}{15}$ | B. | -$\frac{8}{15}$ | C. | $\frac{15}{17}$ | D. | -$\frac{15}{17}$ |
9.已知正三棱锥A-BCD的外接球半径R=$\frac{\sqrt{3}}{2}$,P,Q分别是AB,BC上的点,且满足$\frac{AP}{PB}$=$\frac{CQ}{QB}$=5,DP⊥PQ,则该正三棱锥的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
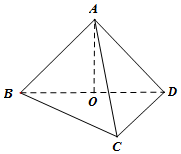 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
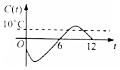
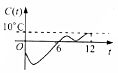
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$, 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )