题目内容
18.已知$α∈({0,\frac{π}{2}}),cosα=\frac{3}{5}$.(1)求$sin({\frac{π}{6}+α})$的值;
(2)若tan(α+β)=3,求tanβ.
分析 (1)利用同角三角函数的基本关系求得sinα的值,利用两角和的正弦公式求得$sin({\frac{π}{6}+α})$的值.
(2)由条件利用两角差的正切公式,求得tanβ的值.
解答 解:(1)$α∈({0,\frac{π}{2}}),cosα=\frac{3}{5}$$⇒sinα=\frac{4}{5}$,
∴$sin({\frac{π}{6}+α})=sin\frac{π}{6}cosα+cos\frac{π}{6}sinα=\frac{1}{2}•\frac{3}{5}+\frac{{\sqrt{3}}}{2}•\frac{4}{5}=\frac{{3+4\sqrt{3}}}{10}$.
(2)由(1)知道$tanα=\frac{4}{3}$,
因为tan(α+β)=3,所以tanβ=tan[(α+β)-α]=$\frac{{3-\frac{4}{3}}}{{1+3×\frac{4}{3}}}=\frac{1}{3}$.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.

练习册系列答案
相关题目
8.如果一个函数f(x)满足:(1)定义域为R;(2)任意x1,x2∈R,若x1+x2=0,则f(x1)+f(x2)=0;(3)任意x∈R,若t>0,总有f(x+t)>f(x),则f(x)可以是( )
| A. | y=-x | B. | y=3x | C. | y=x3 | D. | y=log3x |
6.已知双曲线x2-y2=1,点F1,F2为其两个焦点,点P为双曲线上一点,若P F1⊥PF2,则以F1,F2为焦点且经过P的椭圆的离心率等于( )
| A. | .$\frac{{\sqrt{5}}}{5}$ | B. | .$\frac{{\sqrt{6}}}{3}$ | C. | .$\frac{{\sqrt{2}}}{2}$ | D. | .$\frac{1}{2}$ |
13.-630°化为弧度为( )
| A. | -$\frac{7π}{2}$ | B. | $\frac{7π}{4}$ | C. | -$\frac{7π}{16}$ | D. | -$\frac{7π}{4}$ |
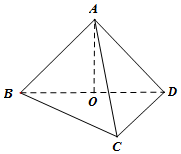 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,