题目内容
18.已知α是第三象限角,且cos(α+π)=$\frac{4}{5}$,则tan2α=$\frac{24}{7}$.分析 利用同角三角函数的基本关系、诱导公式求得tanα的值,再利用二倍角的正切公式,求得tan2α的值.
解答 解:∵α是第三象限角,且cos(α+π)=-cosα=$\frac{4}{5}$,∴cosα=-$\frac{4}{5}$,∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{3}{5}$,
∴tanα=$\frac{sinα}{cosα}$=$\frac{3}{4}$,则tan2α=$\frac{2tanα}{1{-tan}^{2}α}$=$\frac{\frac{3}{2}}{1-\frac{9}{16}}$=$\frac{24}{7}$,
故答案为:$\frac{24}{7}$.
点评 本题主要考查同角三角函数的基本关系、诱导公式、二倍角的正切公式的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.已知正三棱锥A-BCD的外接球半径R=$\frac{\sqrt{3}}{2}$,P,Q分别是AB,BC上的点,且满足$\frac{AP}{PB}$=$\frac{CQ}{QB}$=5,DP⊥PQ,则该正三棱锥的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
13.已知复数z满足(1+i)z=2i,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
3.由表格中的数据可以判定函数f(x)=lnx-x+2的一个零点所在的区间是(k,k+1)(k∈Z),则k的值为( )
| x | 1 | 2 | 3 | 4 | 5 |
| lnx | 0 | 0.69 | 1.10 | 1.39 | 1.61 |
| x-2 | -1 | 0 | 1 | 2 | 3 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.设F为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,过坐标原点的直线依次与双曲线C的左、右支交于点P,Q,若|PQ|=2|QF|,∠PQF=60°,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
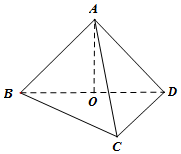 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
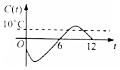
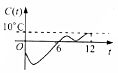
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$, 某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示.已知该年的平均气温为10℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )