题目内容
20.在△ABC中,D是边AB上的中点,记$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{c}$,则向量$\overrightarrow{CD}$=( )| A. | -$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | $\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{c}$ | C. | -$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$ |
分析 根据向量加减的几何意义即可求出.
解答 解:∵D为AB的中点,$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{BA}$=$\overrightarrow{c}$,
∴$\overrightarrow{CD}$=$\overrightarrow{CB}$+$\overrightarrow{BD}$=-$\overrightarrow{BC}$+$\frac{1}{2}$$\overrightarrow{BA}$=-$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{c}$,
故选:C.
点评 本题考查了向量的加减的几何意义,属于基础题.

练习册系列答案
相关题目
11.双曲线$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{3+m}$=1的一个焦点为(2,0),则m的值为( )
| A. | $\frac{1}{2}$ | B. | 1或3 | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
15.定义运算:$a?b=\left\{\begin{array}{l}a,(a>b)\\ b,(a<b)\end{array}\right.$,例如2?3=3,则下列等式不能成立的是( )
| A. | (a?b)2=a2?b2 | B. | (a?b)?c=a?(b?c) | ||
| C. | (a?b)2=(b?a)2 | D. | c•(a?b)=(c•a)?(c•b)(c>0) |
9.已知正三棱锥A-BCD的外接球半径R=$\frac{\sqrt{3}}{2}$,P,Q分别是AB,BC上的点,且满足$\frac{AP}{PB}$=$\frac{CQ}{QB}$=5,DP⊥PQ,则该正三棱锥的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
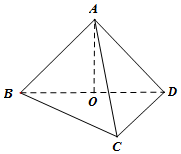 (理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,
(理科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,AC=BC=1,CD=$\sqrt{2}$,