题目内容
19.关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,则实数a的取值范围是( )| A. | $(-∞,-\frac{7}{2})$ | B. | (-∞,1) | C. | $(-\frac{7}{2},+∞)$ | D. | (1,+∞) |
分析 关于x的不等式x2+ax-2<0在区间[1,4]上恒成立?a<($\frac{2}{x}$-x)min,x∈[1,4],利用函数的单调性即可得出.
解答 解:∵关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,
∴a<$\frac{2}{x}$-x,x∈[1,4].
?a<($\frac{2}{x}$-x)min,x∈[1,4],
∵函数f(x)=$\frac{2}{x}$-x在x∈[1,4]单调递减,
∴当x=4时,函数f(x)取得最小值$\frac{2}{4}-4$=-$\frac{7}{2}$.
∴实数a的取值范围为(-∞,-$\frac{7}{2}$).
故选:A.
点评 本题考查了函数的单调性、分离参数法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知集合A={x|x≥3或x≤1},B={x|2<x<4},则(∁RA)∩B=( )
| A. | (1,3) | B. | (1,4) | C. | (2,3) | D. | (2,4) |
9.已知函数f(x)=cos(cosx),下列结论错误的是( )
| A. | f(x)是奇函数 | B. | π为f(x)的最小正周期 | ||
| C. | f(x)的对称轴方程为x=kπ(k∈Z) | D. | f(x)的值域为[cos1,1] |
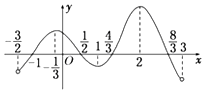 已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].