题目内容
7.已知函数f(x)=ax2+$\frac{2}{x}$(a∈R)为奇函数.(1)比较f(log23)、f(log38)、f(log326)的大小,并说明理由;(提示:log23≈1.59)
(2)若t>0,且f(t+x2)+f(1-x-x2-2x)>0对x∈[2,3]恒成立,求实数t的取值范围.
分析 (1)直接由奇函数的概念列式求得a的值;
(2)先比较得到log326>log38>log23,再根据f(x)=$\frac{2}{x}$在(0,+∞)上递减,即可得到答案,
(3)根据函数为奇函数且为减函数得到t+x2<-1+x+x2+2x,分离参数,得到t<2x+x-1对x∈[2,3]恒成立,再根据函数的单调性即可求出t的范围.
解答 解:(1)∵函数f(x)为奇函数,
∴f(-x)=-f(x),
∴ax2-$\frac{2}{x}$=-(ax2+$\frac{2}{x}$),
∴2ax2=0,对x∈R恒成立,
∴a=0.
∴f(x)=$\frac{2}{x}$.
∵log38<log326,log38=3log32=$\frac{3}{lo{g}_{2}3}$=$\frac{3}{1.59}$≈1.89
∴log38>log23,
∴log326>log38>log23,
∵f(x)=$\frac{2}{x}$在(0,+∞)上递减,
∴f(log326)<f(log38)<f(log23),
(2)由f(x)为奇函数可得f(t+x2)>f(-1+x+x2+2x),
∵t>0,x∈[2,3],
∴t+x2>0,-1+x+x2+2x>0
∵f(x)=$\frac{2}{x}$在(0,+∞)上递减
∴t+x2<-1+x+x2+2x,
即t<2x+x-1对x∈[2,3]恒成立.
∵y=2x+x-1在[2,3]上递增,
∴t<22+2-1=5,
又t>0.
∴0<t<5.
点评 本题考查了函数的性质,训练了数学转化思想方法,考查了利用分离变量法求参数的取值范围,是中档题.

练习册系列答案
相关题目
18.设$a=(\frac{7}{9})^{5}$,$b=(\frac{9}{7})^{\frac{1}{5}}$,$c=lo{g}_{2}\frac{7}{9}$,则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
2.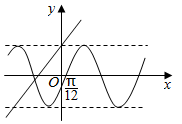 若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
 若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )| A. | x=-$\frac{π}{24}$ | B. | x=$\frac{37π}{24}$ | C. | x=$\frac{17π}{24}$ | D. | x=-$\frac{13π}{24}$ |
12.定义在R上的函数f(x),已知函数y=f(x+1)的图象关于直线x=-1对称,对任意的x1,x2∈(-∞,0)(x1≠x2),都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}<0$,则下列结论正确的是( )
| A. | f(0.32)<f(20.3)<f(log25) | B. | $f({log_2}5)<f({2^{0.3}})<f({0.3^2})$ | ||
| C. | $f({log_2}5)<f({0.3^2})<f({2^{0.3}})$ | D. | $f({0.3^2})<f({log_2}5)<f({2^{0.3}})$ |
19.关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,则实数a的取值范围是( )
| A. | $(-∞,-\frac{7}{2})$ | B. | (-∞,1) | C. | $(-\frac{7}{2},+∞)$ | D. | (1,+∞) |
17.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
| A. | $\stackrel{∧}{y}$=1.23x+5 | B. | $\stackrel{∧}{y}$=1.23x+4 | C. | $\stackrel{∧}{y}$=0.08x+1.23 | D. | $\stackrel{∧}{y}$=1.23x+0.08 |