题目内容
10．已知集合A={x|x≥3或x≤1}，B={x|2＜x＜4}，则（∁RA）∩B=（ ）| A． | （1，3） | B． | （1，4） | C． | （2，3） | D． | （2，4） |
分析 根据补集和交集的定义，写出运算结果即可．
解答 解：∵集合A={x|x≥3或x≤1}，
∴∁RA={x|1＜x＜3}，
又B={x|2＜x＜4}，
∴（∁RA）∩B={x|2＜x＜3}=（2，3）．
故选：C．
点评 本题考查了补集和交集的定义与运算问题，是基础题目．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
20．设集合A={1，2，3，4}，则集合A的真子集的个数为（ ）
| A． | 16 | B． | 15 | C． | 14 | D． | 13 |
1．已知某随机变量X的概率密度函数为$P（x）=\left\{\begin{array}{l}0，x≠0\\{e^{-x}}，x＞0\end{array}\right.$，则随机变量X落在区间（1，3）内的概率为（ ）
| A． | $\frac{e+1}{e^2}$ | B． | $\frac{{{e^2}-1}}{e^3}$ | C． | e2-e | D． | e2+e |
18．设$a=（\frac{7}{9}）^{5}$，$b=（\frac{9}{7}）^{\frac{1}{5}}$，$c=lo{g}_{2}\frac{7}{9}$，则a，b，c的大小关系是（ ）
| A． | b＜a＜c | B． | c＜a＜b | C． | c＜b＜a | D． | b＜c＜a |
2．
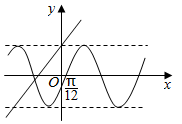若函数y=ksin（kx+φ）（k＞0，|φ|＜$\frac{π}{2}$）与函数y=kx-k2+6的部分图象如图所示，则函数f（x）=sin（kx-φ）+cos（kx-φ）图象的一条对称轴的方程可以为（ ）
若函数y=ksin（kx+φ）（k＞0，|φ|＜$\frac{π}{2}$）与函数y=kx-k2+6的部分图象如图所示，则函数f（x）=sin（kx-φ）+cos（kx-φ）图象的一条对称轴的方程可以为（ ）| A． | x=-$\frac{π}{24}$ | B． | x=$\frac{37π}{24}$ | C． | x=$\frac{17π}{24}$ | D． | x=-$\frac{13π}{24}$ |
19．关于x的不等式x2+ax-2＜0在区间[1，4]上恒成立，则实数a的取值范围是（ ）
| A． | $（-∞，-\frac{7}{2}）$ | B． | （-∞，1） | C． | $（-\frac{7}{2}，+∞）$ | D． | （1，+∞） |