题目内容
9.已知函数f(x)=ln(${\sqrt{1+{x^2}}$-x)+2,则f(lg5)+f(lg$\frac{1}{5}}$)=( )| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
分析 利用对数的运算性质计算f(x)+f(-x)=4,即可得出.
解答 解:∵f(x)=ln(${\sqrt{1+{x^2}}$-x)+2,∴f(x)+f(-x)
=ln(${\sqrt{1+{x^2}}$-x)+2+ln(${\sqrt{1+{x^2}}$+x)+2=lg1+4=4,
则f(lg5)+f(lg$\frac{1}{5}}$)=f(lg5)+f(-lg5)=4.
故选:A.
点评 本题考查了对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
20.设集合A={1,2,3,4},则集合A的真子集的个数为( )
| A. | 16 | B. | 15 | C. | 14 | D. | 13 |
4.若不等式x2+x+a+1≥0对一切$x∈[{0,\frac{1}{2}}]$都成立,则a的最小值为( )
| A. | 0 | B. | -1 | C. | $-\frac{5}{2}$ | D. | $-\frac{7}{4}$ |
1.已知某随机变量X的概率密度函数为$P(x)=\left\{\begin{array}{l}0,x≠0\\{e^{-x}},x>0\end{array}\right.$,则随机变量X落在区间(1,3)内的概率为( )
| A. | $\frac{e+1}{e^2}$ | B. | $\frac{{{e^2}-1}}{e^3}$ | C. | e2-e | D. | e2+e |
18.设$a=(\frac{7}{9})^{5}$,$b=(\frac{9}{7})^{\frac{1}{5}}$,$c=lo{g}_{2}\frac{7}{9}$,则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
19.关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,则实数a的取值范围是( )
| A. | $(-∞,-\frac{7}{2})$ | B. | (-∞,1) | C. | $(-\frac{7}{2},+∞)$ | D. | (1,+∞) |
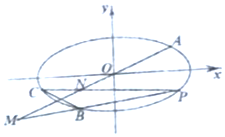 如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.
如图,在平面直角坐标系xOy中,已知A,B,C是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)上不同的三点,$A(\sqrt{10},\frac{{\sqrt{10}}}{2})$,B(-2,-2),C在第三象限,线段BC的中点在直线OA上.