题目内容
14.已知不等式ax2+x+c>0的解集为{x|1<x<3}.(1)求a,c的值;
(2)若不等式ax2+2x+4c>0的解集为A,不等式3ax+cm<0的解集为B,且A?B,求实数m的取值范围.
分析 (1)由一元二次不等式和对应方程的关系,利用根与系数的关系即可求出a、c的值;
(2)由(1)中a、c的值求解不等式ax2+2x+4c>0,再根据真子集的定义求出m的取值范围.
解答 解:(1)∵不等式ax2+x+c>0的解集为{x|1<x<3},
∴1、3是方程ax2+x+c=0的两根,且a<0,…(1分)
所以$\left\{\begin{array}{l}{a<0}\\{1+3=-\frac{1}{a}}\\{1×3=\frac{c}{a}}\end{array}\right.$;…(3分)
解得a=-$\frac{1}{4}$,c=-$\frac{3}{4}$;…(5分)
(2)由(1)得a=-$\frac{1}{4}$,c=-$\frac{3}{4}$,
所以不等式ax2+2x+4c>0化为-$\frac{1}{4}$x2+2x-3>0,
解得2<x<6,
∴A={x|2<x<6},
又3ax+cm<0,即为x+m>0,
解得x>-m,
∴B={x|x>-m},…(8分)
∵A?B,
∴{x|2<x<6}?{x|x>-m},
∴-m≤2,即m≥-2,
∴m的取值范围是[2,+∞).…(10分)
点评 本题考查了一元二次不等式和对应方程的应用问题,也考查了真子集的定义与应用问题,是中档题目.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
4.若不等式x2+x+a+1≥0对一切$x∈[{0,\frac{1}{2}}]$都成立,则a的最小值为( )
| A. | 0 | B. | -1 | C. | $-\frac{5}{2}$ | D. | $-\frac{7}{4}$ |
2.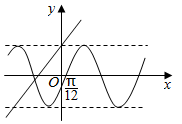 若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
 若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )
若函数y=ksin(kx+φ)(k>0,|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则函数f(x)=sin(kx-φ)+cos(kx-φ)图象的一条对称轴的方程可以为( )| A. | x=-$\frac{π}{24}$ | B. | x=$\frac{37π}{24}$ | C. | x=$\frac{17π}{24}$ | D. | x=-$\frac{13π}{24}$ |
19.关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,则实数a的取值范围是( )
| A. | $(-∞,-\frac{7}{2})$ | B. | (-∞,1) | C. | $(-\frac{7}{2},+∞)$ | D. | (1,+∞) |
3.不等式(2-a)x2-2(a-2)+4>0对于一切实数都成立,则( )
| A. | {a|-2<a≤2} | B. | {a|-2<a<2} | C. | {a|a<-2} | D. | {a|a<-2或a>2} |
4.下列命题的正确的是( )
| A. | 若直线 l上有无数个点不在平面 α内,则 l∥α | |
| B. | 若直线 l与平面α平行,则l与平面α内的任意一条直线都平行 | |
| C. | 如果两条平行直线中的一条与一个平面α平行,那么另一条也与这个平面平行. | |
| D. | 若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点 |