题目内容
8. 已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
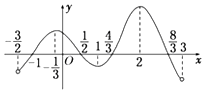
已知函数y=f(x)在定义域(-$\frac{3}{2}$,3)内可导,其图象如图所示.记y=f(x)的导函数为y=f′(x),则不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
分析 不等式$\frac{f′(x)}{x-1}$≤0,等价于$\left\{\begin{array}{l}{f′(x)≤0}\\{x>1}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{f′(x)≥0}\\{x<1}\end{array}\right.$②.根据单调性与导数的关系分别求得①、②的解集,再取并集,即得所求.
解答 解:不等式$\frac{f′(x)}{x-1}$≤0,等价于$\left\{\begin{array}{l}{f′(x)≤0}\\{x>1}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{f′(x)≥0}\\{x<1}\end{array}\right.$②.
由y=f(x)图象可知f(x)在[-$\frac{1}{3}$,1]、[2,3)内递减,f′(x)≤0;
f(x)在(-$\frac{3}{2}$,-$\frac{1}{3}$]、[1,2]内递增,f′(x)≥0.
故由①可得x∈[2,3],由②可得x∈(-$\frac{3}{2}$,-$\frac{1}{3}$].
综上可得,不等式$\frac{f′(x)}{x-1}$≤0的解集为[2,3]∪(-$\frac{3}{2}$,-$\frac{1}{3}$],
故答案为:[2,3)∪(-$\frac{3}{2}$,-$\frac{1}{3}$].
点评 本题主要考查了导数的正负和原函数增减性的问题,导数的符号决定函数的单调性:导数为正,函数单增;导数为负,函数递减,属中档题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
18.设$a=(\frac{7}{9})^{5}$,$b=(\frac{9}{7})^{\frac{1}{5}}$,$c=lo{g}_{2}\frac{7}{9}$,则a,b,c的大小关系是( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
19.关于x的不等式x2+ax-2<0在区间[1,4]上恒成立,则实数a的取值范围是( )
| A. | $(-∞,-\frac{7}{2})$ | B. | (-∞,1) | C. | $(-\frac{7}{2},+∞)$ | D. | (1,+∞) |
3.不等式(2-a)x2-2(a-2)+4>0对于一切实数都成立,则( )
| A. | {a|-2<a≤2} | B. | {a|-2<a<2} | C. | {a|a<-2} | D. | {a|a<-2或a>2} |
17.已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为( )
| A. | $\stackrel{∧}{y}$=1.23x+5 | B. | $\stackrel{∧}{y}$=1.23x+4 | C. | $\stackrel{∧}{y}$=0.08x+1.23 | D. | $\stackrel{∧}{y}$=1.23x+0.08 |