题目内容
已知△ABC内角A、B、C的对边分别为a，b，c，其中A=120°，S△ABC=
，则a的最小值为 ．
| 3 |
考点：正弦定理
专题：解三角形
分析：由题意根据S△ABC=
，求得bc，再由余弦定理可得 a2=b2+c2-2bc•cosA，利用基本不等式求得a的最小值．
| 3 |
解答：
解：由题意可得S△ABC=
=
bc•sinA=
•bc•
，∴bc=4．
再由余弦定理可得 a2=b2+c2-2bc•cosA≥3bc=12，∴a≥2
，
当且仅当b=c时，取等号，故a的最小值为2
，
故答案为：2
．
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
再由余弦定理可得 a2=b2+c2-2bc•cosA≥3bc=12，∴a≥2
| 3 |
当且仅当b=c时，取等号，故a的最小值为2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查正弦定理、基本不等式的应用，属于中档题．
练习册系列答案
计算高手系列答案
相关题目
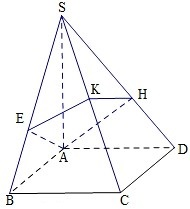如图，四棱锥S-ABCD的底面是正方形，侧棱SA⊥底面ABCD，过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面AEH交SC于K点，且AB=1，SA=2．
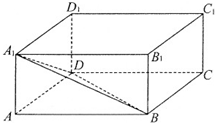如图，长方体ABCD-A1B1C1D1，有一动点在此长方体内随机运动，则此动点在三棱锥A-A1BD内的概率为阅读如图所示的程序框图，运行相应的程序，输出的s值等于（ ）
| A、-3 | B、-21 | C、3 | D、21 |
如图是一个几何体的三视图，则该几何体的体积是（ ）
| A、3 | ||
B、
| ||
| C、1 | ||
D、
|