题目内容
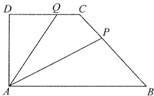如图，在直角梯形ABCD中，AB∥CD，AB=2，AD=DC=1，P是线段BC上一动点，Q是线段DC上一动点，| DQ |
| DC |
| CP |
| CB |
| AP |
| AQ |
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：通过向量的坐标运算转化为二次函数的单调性即可得出．
解答：
解：如图所示，
A（0，0），B（2，0），C（1，1），D（0，1）．
=
+
=（1，1）+（1-λ）
，λ∈[0，1]．
=（1，1）+（1-λ）（1，-1）=（2-λ，λ）．
=
+
=（0，1）+λ
=（0，1）+λ（1，0）=（λ，1）．
∴f（λ）=
•
=（2-λ，λ）•（λ，1）=λ（2-λ）+λ
=-λ2+3λ
=-(λ-
)2+
，
∵λ∈[0，1]，∴f（0）≤f（λ）≤f（1），
∴0≤f（λ）≤2．
∴
•
的取值范围是[0，2]．
故答案为：[0，2]．
A（0，0），B（2，0），C（1，1），D（0，1）．
| AP |
| AC |
| CP |
| CB |
=（1，1）+（1-λ）（1，-1）=（2-λ，λ）．
| AQ |
| AD |
| DQ |
| DC |
∴f（λ）=
| AP |
| AQ |
=-λ2+3λ
=-(λ-
| 3 |
| 2 |
| 9 |
| 4 |
∵λ∈[0，1]，∴f（0）≤f（λ）≤f（1），
∴0≤f（λ）≤2．
∴
| AP |
| AQ |
故答案为：[0，2]．
点评：本题考查了向量的坐标运算、二次函数的单调性，属于基础题．
练习册系列答案
相关题目
设l、m是两条不同的直线，α、β是两个不同的平面，则下列正确的是（ ）
| A、若l⊥α，l⊥β，则α∥β |
| B、若l∥α，α⊥β，则l⊥β |
| C、若l∥m，m∥α，则l∥α |
| D、若α⊥β，α∩β=l，l⊥m，则m⊥α |
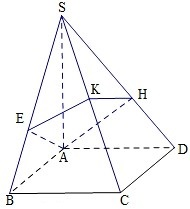如图，四棱锥S-ABCD的底面是正方形，侧棱SA⊥底面ABCD，过A作AE垂直SB交SB于E点，作AH垂直SD交SD于H点，平面AEH交SC于K点，且AB=1，SA=2．
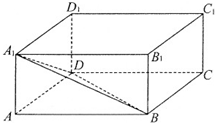如图，长方体ABCD-A1B1C1D1，有一动点在此长方体内随机运动，则此动点在三棱锥A-A1BD内的概率为如图是一个几何体的三视图，则该几何体的体积是（ ）
| A、3 | ||
B、
| ||
| C、1 | ||
D、
|