题目内容
若x、y满足不等式
,则z=3x+y的最大值为( )
|
| A、11 | B、-11 |
| C、13 | D、-13 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据z的几何意义,利用数形结合即可得到最大值.
解答:
解:不等式组对应的平面区域如图:
由z=3x+y得y=-3x+z,
平移直线y=-3x+z,则由图象可知当直线y=-3x+z经过点A时直线y=-3x+z的截距最大,
此时z最大,
此时M=z=3×
+5×
=17, 由
由
,
解得
,即A(4,-1),
此时z=3×4-1=11,
故选:A.
由z=3x+y得y=-3x+z,
平移直线y=-3x+z,则由图象可知当直线y=-3x+z经过点A时直线y=-3x+z的截距最大,
此时z最大,
此时M=z=3×
| 3 |
| 2 |
| 5 |
| 2 |
 由
由
|
解得
|
此时z=3×4-1=11,
故选:A.
点评:本题主要考查线性规划的应用,根据z的几何意义,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
认真阅读如图所示程序框图,则输出的S等于( )


| A、14 | B、20 | C、30 | D、55 |
如图是一个几何体的三视图,则该几何体的体积是( )


| A、3 | ||
B、
| ||
| C、1 | ||
D、
|
设变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、-3 | ||
B、
| ||
| C、6 | ||
| D、10 |
执行如图所示的程序框图,若输入n的值为7,则输出的s的值为( )


| A、22 | B、16 | C、15 | D、11 |

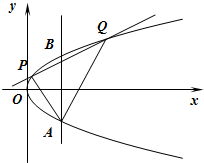 如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=
如图,两条相交线段AB、PQ的四个端点都在抛物线y2=x上,其中,直线AB的方程为x=m,直线PQ的方程为y=