题目内容
已知函数f(x)=
x2-mlnx(m∈R,且m为常数).
(1)讨论函数f(x)的单调性;
(2)求函数f(x)在[1,e]上的最小值.
| 1 |
| 2 |
(1)讨论函数f(x)的单调性;
(2)求函数f(x)在[1,e]上的最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)求导数可得f′(x)=x-
=
,①若m≤0,则f′(x)>0,易得单调递增;②若m>0,由f′(x)=
=0易得函数f(x)在区间(0,
)单调递减,在区间(
,+∞)单调递增;
(2)①若m≤1,函数f(x)在[1,e]上单调递增,函数的最小为f(1);②若1<m<e2,函数f(x)在(1,
)上单调递减,在(
,e)上单调递增,函数的最小为f(
);③若m≥e2,函数f(x)在[1,e]上单调递减,函数的最小为f(e)
| m |
| x |
| x2-m |
| x |
| x2-m |
| x |
| m |
| m |
(2)①若m≤1,函数f(x)在[1,e]上单调递增,函数的最小为f(1);②若1<m<e2,函数f(x)在(1,
| m |
| m |
| m |
解答:
解:(1)∵f(x)=
x2-mlnx,(x>0),
∴f′(x)=x-
=
,
①若m≤0,则f′(x)=
>0,函数f(x)在区间(0,+∞)单调递增;
②若m>0,由f′(x)=
=0可得x=
,
故当x∈(0,
)时,f′(x)<0,当x∈(
,+∞)时,f′(x)>0
∴函数f(x)在区间(0,
)单调递减,在区间(
,+∞)单调递增;
(2)①若m≤1,则当x∈[1,e]时,f′(x)≥0,函数f(x)在[1,e]上单调递增,∴函数的最小为f(1)=
;
②若1<m<e2,则当x∈(1,
)时,f′(x)<0,当x∈(
,e)时,f′(x)>0,
∴函数f(x)在(1,
)上单调递减,在(
,e)上单调递增,
∴函数的最小为f(
)=
-
lnm;
③若m≥e2,则当x∈[1,e]时,f′(x)≤0,函数f(x)在[1,e]上单调递减,∴函数的最小为f(e)=
-m
| 1 |
| 2 |
∴f′(x)=x-
| m |
| x |
| x2-m |
| x |
①若m≤0,则f′(x)=
| x2-m |
| x |
②若m>0,由f′(x)=
| x2-m |
| x |
| m |
故当x∈(0,
| m |
| m |
∴函数f(x)在区间(0,
| m |
| m |
(2)①若m≤1,则当x∈[1,e]时,f′(x)≥0,函数f(x)在[1,e]上单调递增,∴函数的最小为f(1)=
| 1 |
| 2 |
②若1<m<e2,则当x∈(1,
| m |
| m |
∴函数f(x)在(1,
| m |
| m |
∴函数的最小为f(
| m |
| m |
| 2 |
| m |
| 2 |
③若m≥e2,则当x∈[1,e]时,f′(x)≤0,函数f(x)在[1,e]上单调递减,∴函数的最小为f(e)=
| e2 |
| 2 |
点评:本题考查导数法研究函数闭区间上的单调性和最值,分类讨论是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=log
(x+
+5)(x>1)的最大值为( )
| 1 |
| 2 |
| 1 |
| x-1 |
| A、4 | B、3 | C、-4 | D、-3 |
圆C:x2+y2-4=0被直线l:x-y+2=0截得的弦长为( )
A、2
| ||
B、
| ||
C、
| ||
D、2
|
 如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求:
如图,正四棱柱ABCD-A′B′C′D′中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为CC′、DD′上的点,且CF=2GD=2.求: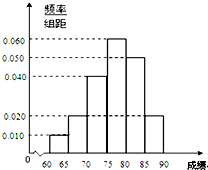 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数