题目内容
16.已知f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,且f(x)满足对任m,n∈[-1,1],有$\frac{f(m)+f(n)}{m+n}$>0.(1)解不等式f(x+$\frac{1}{2}$)+f(x-1)<0;
(2)若f(x)≤t2-2at+1对所有x∈[-1,1]、a∈[-1,1]恒成立,求实数t的取值范围.
(3)若f(x)≤t2-2at+2对所有x∈[-1,1],t∈[-1,1]恒成立,求实数a的取值范围.
分析 (1)先用定义判断f(x)在[-1,1]上的单调性,由函数的单调性、奇偶性可去掉不等式中的符号“f”,解出即可;
(2)对任意的x∈[-1,1]不等式恒成立,等价于f(x)max=f(1))≤t2-2at+1,对任意a∈[-1,1]恒成立,可看作关于a的一次函数,借助图象可得关于a的不等式组,解出即可;
(3)令g(x)=x2-2ax+1,不等式恒成立,转化为$\left\{\begin{array}{l}{a≤1}\\{g(-1)≥0}\end{array}\right.$或$\left\{\begin{array}{l}{a≥1}\\{g(1)≥0}\end{array}\right.$或,$\left\{\begin{array}{l}{-1<a<1}\\{g(a)≥0}\end{array}\right.$,解得即可.
解答 解:(1)∵f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,
m、n∈[-1,1],m≠n时,有$\frac{f(m)+f(n)}{m+n}$>0.
∴任取x1,x2∈[-1,1],且x2≥x1,
则f(x2)-f(x1)=$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$(x2-x1)>0,
∴f(x2)>f(x1),
∴函数f(x)在[-1,1]上单调递增.
∵f(x+$\frac{1}{2}$)+f(x-1)<0,即f(x+$\frac{1}{2}$)<f(1-x),
∴$\left\{\begin{array}{l}{-1≤x+\frac{1}{2}≤1}\\{-1≤x-1≤1}\\{x+\frac{1}{2}<1-x}\end{array}\right.$,解得0≤x<$\frac{1}{4}$,
∴x的取值范围为[0,$\frac{1}{4}$).
(2)由于f(x)为增函数,∴f(x)的最大值为f(1)=1,
∴f(x)≤t2-2at+1对a∈[-1,1]、x∈[-1,1]恒成立,
∴t2-2at+1≥1对任意a∈[-1,1]恒成立,
∴t2-2at≥0对任意a∈[-1,1]恒成立,
把y=t2-2at看作a的函数,
由a∈[-1,1],知其图象是一条线段,
∴t2-2at≥0对任意a∈[-1,1]恒成立,
∴有$\left\{\begin{array}{l}{{t}^{2}-2×(-1)×t≥0}\\{{t}^{2}-2×1×t≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{{t}^{2}+2t≥0}\\{{t}^{2}-2t≥0}\end{array}\right.$,
解得t≤-2,或t=0,或t≥2.
故实数t的取值范围是{t|t≤-2,或t=0,或t≥2}.
(3)∵t2-2at+1≥0,
令g(x)=x2-2ax+1,
∵f(x)≤t2-2at+1对所有x∈[-1,1],t∈[-1,1]恒成立,
∴$\left\{\begin{array}{l}{a≤1}\\{g(-1)≥0}\end{array}\right.$得a=-1,$\left\{\begin{array}{l}{a≥1}\\{g(1)≥0}\end{array}\right.$,得a=1,$\left\{\begin{array}{l}{-1<a<1}\\{g(a)≥0}\end{array}\right.$,解得-1<a<1,
综上所述:-1≤a≤1.
点评 本题考查函数的单调性的判断,考查不等式解集的求法,考查转化思想、数形结合思想.解题时要认真审题,注意定义法、等价转化思想、构造法的合理运用.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | $[-\sqrt{2},\sqrt{2}]$ | B. | $[1,\sqrt{2}]$ | C. | [2,3] | D. | [1,2] |
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
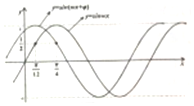
| A. | 沿x轴向左平移$\frac{π}{6}$个单位 | B. | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C. | 沿x轴向右平移$\frac{π}{6}$个单位 | D. | 沿x轴向右平移$\frac{π}{6}$个单位 |
| A. | 充分必要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |