题目内容
8．如图所示y=sin（ωx+φ）的图象可以由y=sinωx的图象沿x轴经怎样的平移得到的（ ）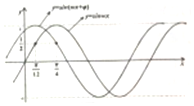
| A． | 沿x轴向左平移$\frac{π}{6}$个单位 | B． | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C． | 沿x轴向右平移$\frac{π}{6}$个单位 | D． | 沿x轴向右平移$\frac{π}{6}$个单位 |
分析 利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．
解答 解：如图所示，∵$\frac{π}{4}$-$\frac{π}{12}$=$\frac{π}{6}$，
故y=sin（ωx+φ）的图象可以由y=sinωx的图象沿x轴向左平移$\frac{π}{6}$个单位得到的，
故选：A．
点评 本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
3．已知变量x，y满足约束条件$\left\{\begin{array}{l}x-y≥1\\ x+y≥1\\ 2x-y≤4\end{array}\right.$，则$z=\frac{{{y^2}+\frac{1}{3}xy+{x^2}}}{x^2}$的最大值与最小值的比值 为（ ）
| A． | $\frac{12}{7}$ | B． | $\frac{77}{75}$ | C． | $\frac{95}{36}$ | D． | $\frac{125}{77}$ |
18．设x，y满足约束条件$\left\{\begin{array}{l}{x≥y}\\{y≥4x-3}\\{x≥0，y≥0}\end{array}\right.$，若目标函数$z=x+\frac{n}{2}y（{n＞0}）$，z最大值为2，则$y=tan（{nx+\frac{π}{6}}）$的图象向右平移$\frac{π}{6}$后的表达式为（ ）
| A． | $y=tan（{2x+\frac{π}{6}}）$ | B． | $y=cot（{x-\frac{π}{6}}）$ | C． | $y=tan（{2x-\frac{π}{6}}）$ | D． | y=tan2x |