题目内容
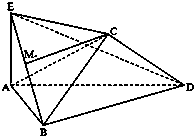将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE=| 2 |
（1）求证：AC⊥面BDE；
（2）求证：CM∥平面ADE．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）要证AC⊥面BDE，关键证明BD⊥AC，AC⊥EF，由线面垂直的判定得证；
（2）通过面面平行来证线面平行，关键证明面MFC∥面ADE．
（2）通过面面平行来证线面平行，关键证明面MFC∥面ADE．
解答：
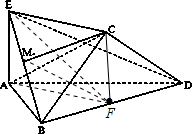证明：（1）F为BD的中点，连接AF、EF，由题意，BD⊥AF，BD⊥CF，AF∩CF=F，∴BD⊥面AFC，AC?面AFC，∴BD⊥AC，
∵平面ABD⊥平面CBD，CF⊥BD，∴CF⊥面ABD，由题意，AF=CF=
，又∵AE⊥平面ABD，AE=
，∴正方形AFCE，∴AC⊥EF，EF?面BDE，BD?面BDE，EF∩BD=F，∴AC⊥面BDE；
（2）M为BE中点，F为BD中点，∴MF∥DE，又由（1）知，正方形AFCE，∴CF∥AE，MF、CF?面MFC，MF∩CF=F，AE、ED?面ADE，AE∩ED=E，∴面MFC∥面ADE，CM?面MFC，CM∥平面ADE．
证明：（1）F为BD的中点，连接AF、EF，由题意，BD⊥AF，BD⊥CF，AF∩CF=F，∴BD⊥面AFC，AC?面AFC，∴BD⊥AC，∵平面ABD⊥平面CBD，CF⊥BD，∴CF⊥面ABD，由题意，AF=CF=
| 2 |
| 2 |
（2）M为BE中点，F为BD中点，∴MF∥DE，又由（1）知，正方形AFCE，∴CF∥AE，MF、CF?面MFC，MF∩CF=F，AE、ED?面ADE，AE∩ED=E，∴面MFC∥面ADE，CM?面MFC，CM∥平面ADE．
点评：本题考查线面垂直及线面平行的判定，构造判定定理的条件是关键．
练习册系列答案
相关题目
