题目内容
已知双曲线C:
-
=1(a>0,b>0)的焦距为2c,焦点到双曲线C的渐近线的距离为
,则双曲线C的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| 2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,双曲线焦点到渐近线的距离为b=
,又b2=c2-a2,代入得4a2=3c2,即可求得双曲线C的离心率.
| c |
| 2 |
解答:
解:由题意,双曲线焦点到渐近线的距离为b=
,
又b2=c2-a2,代入得4a2=3c2,解得e2=
,即e=
,
故选D.
| c |
| 2 |
又b2=c2-a2,代入得4a2=3c2,解得e2=
| 4 |
| 3 |
2
| ||
| 3 |
故选D.
点评:本题考查双曲线的简单性质,考查双曲线中几何量之间的关系,考查数形结合的能力,属于基础题.

练习册系列答案
相关题目
已知{an}是等比数列,a1=2,a4=16,则公比q等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
直线
(t为参数)的倾斜角为( )
|
| A、30° | B、60° |
| C、90° | D、135° |
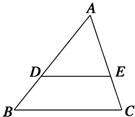 如图所示,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且
如图所示,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且| AD |
| DB |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i是虚数单位,则
=( )
| 2+i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知x与y之间的一组数据如下表所示,则y与x的线性回归方程y=bx+a必经过点( )
| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 1.1 | 1.7 | 5.6 | 6.2 | 7.4 | 9.5 |
| A、(4,5.35) |
| B、(4,5.25) |
| C、(5,5.591) |
| D、(3,5.6) |
 函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )
函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )| A、[-1,0) |
| B、[-2,-1)∪(0,2] |
| C、[-2,-1]∪(0,2] |
| D、[-2,0)∪(0,1] |
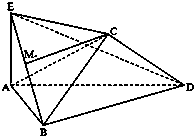 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=