题目内容
已知
=(1,1),
=(1,-2)
(1)求
+2
;
(2)若|
|=1,且
-
与
-2
垂直,求
与
的夹角θ的余弦值.
| a |
| b |
(1)求
| a |
| b |
(2)若|
| c |
| a |
| c |
| a |
| c |
| a |
| c |
考点:数量积表示两个向量的夹角,平面向量数量积的运算
专题:平面向量及应用
分析:(1)由已知和平面向量的坐标运算易得
+2
;(2)由垂直可得(
-
)•(
-2
)=0,代入数据可解cosθ
| a |
| b |
| a |
| c |
| a |
| c |
解答:
解:(1)∵
=(1,1),
=(1,-2),
∴
+2
=(1,1)+2(1,-2)=(3,-3);
(2)∵|
|=1,且
-
与
-2
垂直,
∴(
-
)•(
-2
)=
2-3
•
+2
2=0,
代入数据可得2-3×
×1×cosθ+2×12=0
解得cosθ=
,
∴
与
的夹角θ的余弦值为
| a |
| b |
∴
| a |
| b |
(2)∵|
| c |
| a |
| c |
| a |
| c |
∴(
| a |
| c |
| a |
| c |
| a |
| a |
| c |
| c |
代入数据可得2-3×
| 2 |
解得cosθ=
2
| ||
| 3 |
∴
| a |
| c |
2
| ||
| 3 |
点评:本题考查平面向量的数量积和夹角,属基础题.

练习册系列答案
相关题目
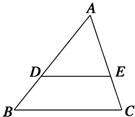 如图所示,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且
如图所示,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且| AD |
| DB |
A、
| ||
B、
| ||
C、
| ||
D、
|
为了判断甲乙两名同学本学期几次数学考试成绩哪个比较稳定,通常需要知道这两个人的( )
| A、平均数 | B、众数 |
| C、方差 | D、频率分布 |
 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE= 设点M,N分别是曲线ρ+2sinθ=0和ρsin(θ+
设点M,N分别是曲线ρ+2sinθ=0和ρsin(θ+