题目内容
某商场对每天进店的人数和商品销售进行统计对比,得到如下表格:
其中i=1,2,3,4,5,6,7
(1)求回归直线方程(结果保留到小数点后两位)
a=
-b
,b=
;或a=
-b
,b=
参考数据:
xiyi=3245,
=25,
=15.43,
xi2=5075,7
2=4375,7
=2700
(2)预测进店人数为80人时,商品销售的件数(结果保留整数).
| 人数xi | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| 件数yi | 4 | 7 | 12 | 15 | 20 | 23 | 27 |
(1)求回归直线方程(结果保留到小数点后两位)
a=
. |
| y |
. |
| x |
| |||||||
|
. |
| y |
. |
| x |
| |||||||
|
参考数据:
| 7 |
 |
| i=1 |
. |
| x |
. |
| y |
| 7 |
 |
| i=1 |
. |
| x |
. |
| x |
. |
| y |
(2)预测进店人数为80人时,商品销售的件数(结果保留整数).
考点:线性回归方程
专题:计算题,概率与统计
分析:(1)根据所给的数据,做出x,y的平均数,即得到这组数据的样本中心点,根据最小二乘法做出线性回归方程的系数,写出线性回归方程.
(2)利用上一问做出的线性回归方程,把x的值代入方程,预报出对应的y的值.
(2)利用上一问做出的线性回归方程,把x的值代入方程,预报出对应的y的值.
解答:
解:(1)∵
xiyi=3245,
=25,
=15.43,
xi2=5075,7
2=4375,7
=2700
∴b≈0.79,a=
-b
=-4.32,
∴回归直线方程是y=0.79x-4.32;
(2)进店人数80人时,商品销售的件数y=0.79×80-4.32≈59件.
| 7 |
 |
| i=1 |
. |
| x |
. |
| y |
| 7 |
 |
| i=1 |
. |
| x |
. |
| x |
. |
| y |
∴b≈0.79,a=
. |
| y |
. |
| x |
∴回归直线方程是y=0.79x-4.32;
(2)进店人数80人时,商品销售的件数y=0.79×80-4.32≈59件.
点评:本题考查线性回归方程,考查最小二乘法求线性回归方程的系数,考查样本中心点的求法,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )
函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )| A、[-1,0) |
| B、[-2,-1)∪(0,2] |
| C、[-2,-1]∪(0,2] |
| D、[-2,0)∪(0,1] |
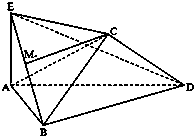 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE= 设点M,N分别是曲线ρ+2sinθ=0和ρsin(θ+
设点M,N分别是曲线ρ+2sinθ=0和ρsin(θ+