题目内容
已知在等比数列{an}中,a1=1,且a2是a1和a3-1的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1+
+
+…+
=an(n∈N*),求{bn}的通项公式bn;
(Ⅲ)求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
(Ⅲ)求数列{bn}的前n项和Sn.
考点:数列的求和,等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:(I)设等比数列{an}的公比为q,由a2是a1和a3-1的等差中项,a1=1,知2a2=a1+(a3-1)=a3,由此能求出数列{an}的通项公式.
(Ⅱ)由b1+
+
+…+
=2n-1,得b1+
+
+…+
=2n-2,两式相减能求出bn=n•2n-2.
(Ⅲ)由bn=n•2n-2,利用错位相减法能求出数列{bn}的前n项和Sn.
(Ⅱ)由b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
| b2 |
| 2 |
| b3 |
| 3 |
| bn-1 |
| n-1 |
(Ⅲ)由bn=n•2n-2,利用错位相减法能求出数列{bn}的前n项和Sn.
解答:
解:(Ⅰ)设等比数列{an}的公比为q,
∵a2是a1和a3-1的等差中项,a1=1,
∴2a2=a1+(a3-1)=a3,
∴q=
=2,
∴an=a1qn-1=2n-1,(n∈N*).
(Ⅱ)∵b1+
+
+…+
=an(n∈N*),
∴b1+
+
+…+
=2n-1,①
∴b1+
+
+…+
=2n-2.②
①-②,得
=2n-2.
∴bn=n•2n-2.
(Ⅲ)∵bn=n•2n-2,
∴Sn=1•2-1+2•20+3×2+…+n•2n-2,③
2Sn=1•20+2×2+3×22+…+n•2n-1,④
③-④,得-Sn=
+1+2+22+…+2n-2-n•2n-1
=
+
-n•2n-1
=
+2n-1-1-n•2n-1,
∴Sn=(n-1)•2n-1+
.
∵a2是a1和a3-1的等差中项,a1=1,
∴2a2=a1+(a3-1)=a3,
∴q=
| a3 |
| a2 |
∴an=a1qn-1=2n-1,(n∈N*).
(Ⅱ)∵b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
∴b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn |
| n |
∴b1+
| b2 |
| 2 |
| b3 |
| 3 |
| bn-1 |
| n-1 |
①-②,得
| bn |
| n |
∴bn=n•2n-2.
(Ⅲ)∵bn=n•2n-2,
∴Sn=1•2-1+2•20+3×2+…+n•2n-2,③
2Sn=1•20+2×2+3×22+…+n•2n-1,④
③-④,得-Sn=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1-2n-1 |
| 1-2 |
=
| 1 |
| 2 |
∴Sn=(n-1)•2n-1+
| 1 |
| 2 |
点评:本题考查等差数列的通项公式的求法和数列求和的应用,解题时要认真审题,仔细解答,熟练掌握等差数列和等比数列的通项公式和前n项和公式的灵活运用.

练习册系列答案
相关题目
直线
(t为参数)的倾斜角为( )
|
| A、30° | B、60° |
| C、90° | D、135° |
 函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )
函数f(x)的定义域为[-2,0)∪(0,2],图象如图,则不等式f(x)-f(-x)≤4的解集是( )| A、[-1,0) |
| B、[-2,-1)∪(0,2] |
| C、[-2,-1]∪(0,2] |
| D、[-2,0)∪(0,1] |
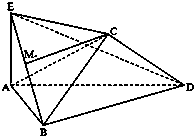 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=