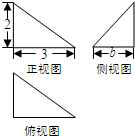
题目内容
已知命题p：方程x2+mx+1=0有两个不相等的负实根，命题q：函数f（x）=mx3+3x2-x+1在R上是减函数恒成立；若p或q为真，p且q为假，求实数m的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：求出命题p为真时m的取值范围，命题q为真时m的取值范围；
由p或q为真，p且q为假得“p为真q为假，或q为真p为假”，从而求出m的取值范围．
由p或q为真，p且q为假得“p为真q为假，或q为真p为假”，从而求出m的取值范围．
解答：
解：∵命题p：方程x2+mx+1=0有两个不相等的负实根，
∴
，解得m＞2；
∵命题q：函数f（x）=mx3+3x2-x+1在R上是减函数恒成立，
∴
，即
，解得m≤-3；
又∵p或q为真，p且q为假，
∴当p为真q为假时，
，即m＞2；
当q为真p为假时，
，解得m≤-3；
综上，m的取值范围是{m|m≤-3，或m＞2}．
∴
|
∵命题q：函数f（x）=mx3+3x2-x+1在R上是减函数恒成立，
∴
|
|
又∵p或q为真，p且q为假，
∴当p为真q为假时，
|
当q为真p为假时，
|
综上，m的取值范围是{m|m≤-3，或m＞2}．
点评：本题通过复合命题的真假，考查了一元二次方程根的情况以及利用函数的导数判定函数的单调性问题，是综合题目．
练习册系列答案
相关题目
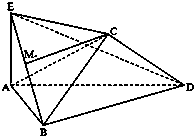将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE=