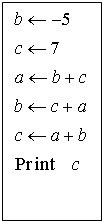题目内容
已知定义在R上的函数f(x),对于任意的x都:f(2-x)=f(2+x),f(4+x)=-f(4-x),求f(0)的值;判断f(x)的奇偶性并证明你的结论.
考点:函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:在f(2-x)=f(2+x)中,令x=2可得f(0)=f(4),在f(4+x)=-f(4-x)中,令x=0可得f(4)=0,从而可得f(0);f(4+x)=-f(4-x)可化为f(2+2-x)=-f(2+2+x),再利用f(2-x)=f(2+x)进行变形可得结论.
解答:
解:由已知f(2-x)=f(2+x),
令x=2,得f(0)=f(2+2)=f(4),
由f(4+x)=-f(4-x),
令x=0,得f(4)=-f(4),即f(4)=0,
∴f(0)=f(4)=0,即f (0)=0;
f(x)为奇函数,证明如下:
由f(4+x)=-f(4-x)⇒f(2+2-x)=-f(2+2+x),
又∵f(2-x)=f(2+x),
∴f(2+2-x)=f[2-(2-x)]=f(x)=-f(2+2+x)=-f[2-(2+x)]=-f(-x),
∴f(-x)=-f(x),即函数f(x)是奇函数.
令x=2,得f(0)=f(2+2)=f(4),
由f(4+x)=-f(4-x),
令x=0,得f(4)=-f(4),即f(4)=0,
∴f(0)=f(4)=0,即f (0)=0;
f(x)为奇函数,证明如下:
由f(4+x)=-f(4-x)⇒f(2+2-x)=-f(2+2+x),
又∵f(2-x)=f(2+x),
∴f(2+2-x)=f[2-(2-x)]=f(x)=-f(2+2+x)=-f[2-(2+x)]=-f(-x),
∴f(-x)=-f(x),即函数f(x)是奇函数.
点评:本题考查函数奇偶性的判断,属中档题,定义是解决奇偶性的基本方法,准确理解已知等式并能灵活运用是解决问题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
对具有线性相关关系的变量x,y有一组观测数据(xi,yi)( i=1,2,…,8),其回归直线方程是
=
x+a且x1+x2+…+x8=6,y1+y2+…+y8=3,则实数a的值是( )
| ? |
| y |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
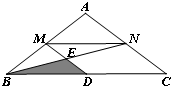 如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )
如图所示,在△ABC中,AB=AC=10cm,BC=16cm,M、N、D分别是AB、AC、BC的中点,连接DM、BN交于点E,则图中阴影部分△BDE的面积为( )| A、4cm2 |
| B、6cm2 |
| C、8cm2 |
| D、12cm2 |