题目内容
10.已知实数x,y满足$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}\right.$,则z=y-2x的最大值是( )| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
分析 先画出满足条件的平面区域,由z=y-2x得;y=2x+z,由图象得直线y=2x+z过A(-2,2)时取到最大值,求出z的最大值即可.
解答 解:画出满足条件$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}\right.$的平面区域,如图示: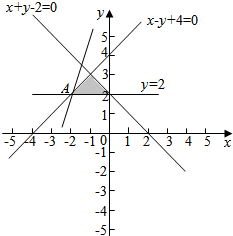
由$\left\{\begin{array}{l}{y=2}\\{x-y+4=0}\end{array}\right.$,解得:A(-2,2),
由z=y-2x得;y=2x+z,
由图象得直线y=2x+z过A(-2,2)时取到最大值,
z的最大值是:6,
故选:D.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道基础题.

练习册系列答案
相关题目
20.点P在边长为2的正方形ABCD内运动,则动点P到定点A的距离|PA|<1的概率为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
5.“a<2”是“实系数一元二次方程x2+ax+1=0有虚根”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知锐角α的终边上一点P(sin40°,cos40°),则α等于( )
| A. | 20° | B. | 40° | C. | 50° | D. | 80° |
19.已知不等式ax2+bx+c<0的解集为(1,2),则不等式$\frac{ax-b}{cx+a}$<0的解集为( )
| A. | (-∞,$\frac{1}{2}$)∪(3,+∞)) | B. | ($\frac{1}{2}$,3) | C. | (-3,-$\frac{1}{2}$) | D. | (-∞,-3)$∪(-\frac{1}{2},+∞)$ |
20.空间四边形ABCD中,每条边长及对角线长都是a,E,F分别是AD、AC的中点,则$\overrightarrow{FE}$•$\overrightarrow{CE}$等于( )
| A. | $\frac{3}{8}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{3}}{8}$a2 | D. | $\frac{3}{4}$a2 |