题目内容

18．若集合A={x||x-1|＜2}，B={x|$\frac{x-2}{x+4}$＜0}，则A∩B=（-1，2）．

分析 求出A与B中不等式的解集确定出A与B，找出两集合的交集即可．

解答 解：由A中不等式变形得：-2＜x-1＜2，即-1＜x＜3，
∴A=（-1，3），
由B中不等式变形得：（x-2）（x+4）＜0，
解得：-4＜x＜2，即B=（-4，2），
则A∩B=（-1，2），
故答案为：（-1，2）

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
8．三棱锥A-BCD的三条侧棱两两互相垂直，且$AB=2，AD=\sqrt{3}，AC=1$，则A，B两点在三棱锥的外接球上的球面距离为$\frac{{\sqrt{2}π}}{2}$．
9．如图，四边形EFGH为四面体A-BCD的一个截面，若截面为平行四边形，
（1）求证：AB∥平面EFGH；
（2）若AB⊥CD，求证：四边形EFGH为矩形．
6．已知数列{an}的各项均为正整数，其前n项和为Sn，若an+1=$\left\{\begin{array}{l}{\frac{{a}_{n}}{2}，}&{{a}_{n}是偶数}\\{{3a}_{n}+1，}&{{a}_{n}是奇数}\end{array}\right.$且a1为一奇数，S3=29，则S2015=4725．
13．如果集合A={x|x=2kπ+π，k∈Z}，B={x|x=4kπ+π，k∈Z}，则（　　）
A．A⊆BB．B⊆AC．A=BD．A∩B=ϕ
3．在矩形ABCD中，AB=2，AD=1，边DC（包含点D、C）的动点P与CB延长线上（包含点B）的动点Q满足|$\overrightarrow{DP}$|=|$\overrightarrow{BQ}$|，则$\overrightarrow{PA}$•$\overrightarrow{PQ}$的取值范围是$[\frac{3}{4}，3]$．
10．已知实数x，y满足$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}\right.$，则z=y-2x的最大值是（　　）
A．2B．4C．5D．6
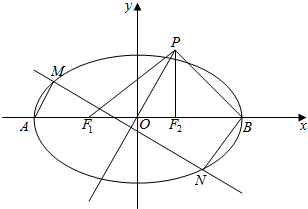7．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的左右焦点分别是F1，F2，左、右顶点分别为A、B，焦距为2c，O为坐标原点，点P（c，b）满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$，|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在直线l：y=kx+m与椭圆C交于M、N两点，使得直线PO平分线段MN，且$\overrightarrow{AM}$=λ$\overrightarrow{BN}$？若存在，求l的方程；若不存在，说明理由．
8．已知数列{an}为等比数列，其前n项和为Sn，已知a1+a4=-$\frac{7}{16}$，且S1，S3，S2成等差，
（1）求数列{an}的通项公式；
（2）已知bn=$\frac{n}{|{a}_{n}|}$（n∈N+），记Tn=b1+b2+b3+…bn，若（n-1）2≤m（Tn-n-1）对于n≥2恒成立，求实数m的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网