题目内容
19.已知不等式ax2+bx+c<0的解集为(1,2),则不等式$\frac{ax-b}{cx+a}$<0的解集为( )| A. | (-∞,$\frac{1}{2}$)∪(3,+∞)) | B. | ($\frac{1}{2}$,3) | C. | (-3,-$\frac{1}{2}$) | D. | (-∞,-3)$∪(-\frac{1}{2},+∞)$ |
分析 根据一元二次不等式的解集与一元二次方程之间的关系求出a,b,c的关系,然后利用分式不等式的性质进行求解.
解答 解:∵不等式ax2+bx+c<0的解集为(1,2),
∴1,2是对应方程ax2+bx+c=0的两个根,且a>0,
则1+2=-$\frac{b}{a}$=3,即b=-3a,1×2=$\frac{c}{a}$=2,即c=2a,
则不等式$\frac{ax-b}{cx+a}$<0等价为$\frac{ax+3a}{2ax+a}$=$\frac{x+3}{2x+1}$<0,
则-3<x<-$\frac{1}{2}$,
即不等式的解集为(-3,-$\frac{1}{2}$),
故选:C
点评 本题主要考查不等式的求解,结合一元二次不等式以及分式不等式的性质和解法是解决本题的关键.

练习册系列答案
相关题目
10.已知实数x,y满足$\left\{\begin{array}{l}x-y+4≥0\\ x+y-2≤0\\ y-2≥0\end{array}\right.$,则z=y-2x的最大值是( )
| A. | 2 | B. | 4 | C. | 5 | D. | 6 |
2.函数f(x)=$\left\{\begin{array}{l}{2{x}^{2}(0≤x<1)}\\{2(1≤x<2)}\\{3(x≥2)}\end{array}\right.$的值域是( )
| A. | R | B. | [0,+∞) | C. | [0,3] | D. | [0,2]∪{3} |
 如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,
如图,四边形EFGH为四面体A-BCD的一个截面,若截面为平行四边形,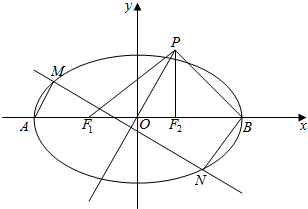 椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.
椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点分别是F1,F2,左、右顶点分别为A、B,焦距为2c,O为坐标原点,点P(c,b)满足$\overrightarrow{PO}$+$\overrightarrow{PB}$=2$\overrightarrow{P{F}_{2}}$,|$\overrightarrow{P{F}_{1}}$|=$\sqrt{7}$.