题目内容
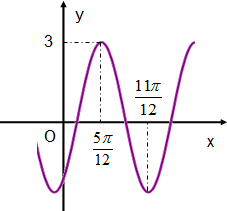 已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-
已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
(1)求该函数的解析式;
(2)求该函数的增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)根据函数的图象确定A,ω 和φ的值即可求该函数的解析式;
(2)根据三角函数的单调性即可求该函数的增区间.
(2)根据三角函数的单调性即可求该函数的增区间.
解答:
解:(1)由图知:A=3 …(1分)
=
-
=
,∴T=π,ω=2…(3分)
又由ω
+ϕ=
得:ϕ=-
,…(5分)
∴所求解析式为:y=3sin(2x-
)…(6分)
(2)令2kπ-
≤2x-
≤2kπ+
(k∈Z)…(8分)
得:kπ-
≤x≤kπ+
,
∴所求增区间是[kπ-
,kπ+
](k∈Z)…(10分)
| T |
| 2 |
| 11π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
又由ω
| 5π |
| 12 |
| π |
| 2 |
| π |
| 3 |
∴所求解析式为:y=3sin(2x-
| π |
| 3 |
(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得:kπ-
| π |
| 12 |
| 5π |
| 12 |
∴所求增区间是[kπ-
| π |
| 12 |
| 5π |
| 12 |
点评:本题主要考查三角函数解析式的求解,利用条件确定A,ω 和φ的值是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)=log2x+logx2k在[2,4]上是单调函数,则实数k的取值范围是( )
| A、1≤k≤4 | B、k≤1 |
| C、k≥4 | D、k≤1或k≥4 |
古希腊数学家把数1,3,6,10,15,21…叫作三角形数,它们有一定的规律性,则第22个三角形数为( )
| A、210 | B、276 |
| C、231 | D、253 |
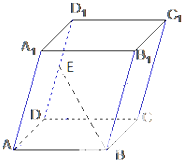 如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设
如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设