题目内容
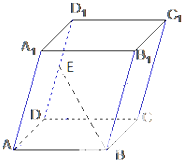 如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设
如图,在平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=4,∠DAB=90°∠BAA1=∠DAA1=60°E是DD的中点,设| AB |
| a |
| AD |
| b |
| AA1 |
| c |
(Ⅰ)用
| a |
| b |
| c |
| BE |
(Ⅱ)求BE的长.
考点:空间两点间的距离公式
专题:计算题,空间位置关系与距离
分析:(Ⅰ)利用向量的加法,即可用
,
,
表示
;
(Ⅱ)|
|2=(
-
+
)2,即可求BE的长.
| a |
| b |
| c |
| BE |
(Ⅱ)|
| BE |
| b |
| a |
| 1 |
| 2 |
| c |
解答:
解:(Ⅰ)
=
+
=-
+
+
=
-
+
…(5分)
(Ⅱ)|
|2=(
-
+
)2…(7分)
=
2+
2+
2-2
•
+
•
-
•
…(9分)
=25+9+4-0+6-10=34…(11分)
即BE的长为
…(12分)
| BE |
| BA |
| AE |
| a |
| AD |
| 1 |
| 2 |
| DD1 |
| b |
| a |
| 1 |
| 2 |
| c |
(Ⅱ)|
| BE |
| b |
| a |
| 1 |
| 2 |
| c |
=
| a |
| b |
| 1 |
| 4 |
| c |
| a |
| b |
| b |
| c |
| a |
| c |
=25+9+4-0+6-10=34…(11分)
即BE的长为
| 34 |
点评:本题考查向量的加法,考查BE的长,正确用
,
,
表示
是关键.
| a |
| b |
| c |
| BE |

练习册系列答案
相关题目
等比数列{an}中,前n项和Sn=
+x,则x的值为( )
| 2n |
| 4 |
A、-
| ||
| B、-4 | ||
| C、-1 | ||
| D、4 |
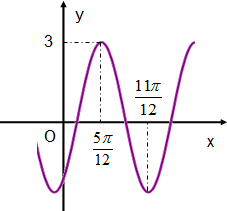 已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-
已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-