题目内容
f(
+1)=x+6
,则f(x)= .
| x |
| x |
考点:函数解析式的求解及常用方法
专题:计算题
分析:由题意设t=
+1,求出t的范围和
,代入关系式化简即可.
| x |
| x |
解答:
解:由题意设t=
+1(t≥1),则
=t-1,
代入f(
+1)=x+6
得,
f(t)=(t-1)2+6(t-1)=t2+4t-5,
所以f(x)=x2+4x-5(x≥1)
故答案为:x2+4x-5(x≥1).
| x |
| x |
代入f(
| x |
| x |
f(t)=(t-1)2+6(t-1)=t2+4t-5,
所以f(x)=x2+4x-5(x≥1)
故答案为:x2+4x-5(x≥1).
点评:本题考查求函数解析式的方法:换元法,注意求出函数的定义域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(x-4,1),
=(x+5,y),x,y∈(0,+∞),且
∥
,则xy取最小值时y的值为( )
| a |
| b |
| a |
| b |
| A、3 | ||
B、
| ||
| C、2 | ||
| D、1 |
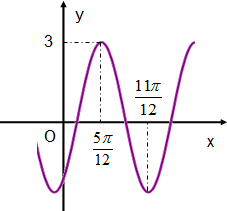 已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-
已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-