题目内容
已知函数f(x)=log2x+logx2k在[2,4]上是单调函数,则实数k的取值范围是( )
| A、1≤k≤4 | B、k≤1 |
| C、k≥4 | D、k≤1或k≥4 |
考点:函数单调性的判断与证明
专题:函数的性质及应用,导数的综合应用
分析:先用换底公式求出f(x)=log2x+
,求f′(x)=
,所以根据题意便有,k≤log22x,或k≥log22x,在[2,4]上恒成立,根据函数log22x在[2,4]上的最大值,最小值即可求出k的取值范围.
| k |
| log2x |
| log22x-k |
| xlog22x•ln2 |
解答:
解:f(x)=log2x+
;
∴f′(x)=
;
∵f(x)在[2,4]上是单调函数;
∴k≤log22x,或k≥log22x在[2,4]上恒成立;
log22x在[2,4]上的最小值为1,最大值为4;
∴k≤1,或k≥4.
故选D.
| k |
| log2x |
∴f′(x)=
| log22x-k |
| xlog22x•ln2 |
∵f(x)在[2,4]上是单调函数;
∴k≤log22x,或k≥log22x在[2,4]上恒成立;
log22x在[2,4]上的最小值为1,最大值为4;
∴k≤1,或k≥4.
故选D.
点评:考查对数的换底公式,单调函数的导数的取值情况,对数函数的单调性,注意正确求导.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中正确的是( )
A、x+
| ||||
B、
| ||||
C、
| ||||
D、6─x─
|
等比数列{an}中,前n项和Sn=
+x,则x的值为( )
| 2n |
| 4 |
A、-
| ||
| B、-4 | ||
| C、-1 | ||
| D、4 |
要得到函数y=cos
x的图象,只要将函数y=cos(
x+1)的图象( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、向左平移2个单位 | ||
| B、向右平移2个单位 | ||
C、向左平移
| ||
D、向右平移
|
两直线ax+by+m=0与ax+by+n=0的距离是( )
| A、|m-n| | ||||
B、
| ||||
C、
| ||||
D、
|
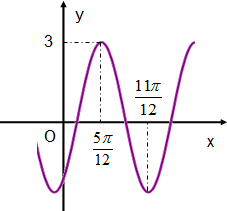 已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-
已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-