题目内容
某化工厂生产的某种化工产品,其年生产的总成本y(万元)与年产量x(吨)之间的关系可近似地表示为y=
-30x+4000,若每吨平均出厂价为16万元,求年生产多少吨时,可获得最大的年利润?并求最大年利润.
| x2 |
| 10 |
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:利用收入减去总成本表示出年利润,通过配方求出二次函数的对称轴,由于开口向下,对称轴处取得最大值.
解答:
解:设年利润为u(万元),则u=16x-y=16x-(
-30x+4000) …4分
=-
+46x-4000=-
(x-230)2+1290…4分
当年产量为230吨时,年利润最大为1290万元 …10分
| x2 |
| 10 |
=-
| x2 |
| 10 |
| 1 |
| 10 |
当年产量为230吨时,年利润最大为1290万元 …10分
点评:本题考查将实际问题的最值问题转化为函数的最值问题,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
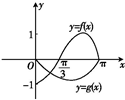 已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式
已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式| f(x) |
| g(x) |
A、(-
| ||||||
B、(
| ||||||
C、(-
| ||||||
D、(-
|
两直线ax+by+m=0与ax+by+n=0的距离是( )
| A、|m-n| | ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}为等比数列,且a3a9=2a52,a2=2,则a1等于( )
A、±
| ||
B、
| ||
C、-
| ||
| D、2 |
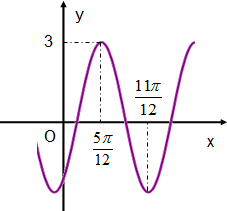 已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-
已知函数y=Asin(ωx+ϕ)(其中A>0,ω>0,-