题目内容
一个扇形的面积为4cm2,周长为8cm,求扇形的圆心角及相应的弦长.
考点:扇形面积公式
专题:三角函数的求值
分析:设扇形的圆心角为α,半径为r.由于扇形的面积为4cm2,周长为8cm,可得
•αr2=4,2r+αr=8,解出即可得出.
| 1 |
| 2 |
解答:
解:设扇形的圆心角为α,半径为r.
∵扇形的面积为4cm2,周长为8cm,
∴
•αr2=4,2r+αr=8,
解得α=2,r=2.
弦长=4sin1.
因此扇形的圆心角为2,相应的弦长为4sin1.
∵扇形的面积为4cm2,周长为8cm,
∴
| 1 |
| 2 |
解得α=2,r=2.
弦长=4sin1.
因此扇形的圆心角为2,相应的弦长为4sin1.
点评:本题考查了扇形的面积计算公式、弧长公式、弦长的计算方法,考查了计算能力,属于基础题.

练习册系列答案
相关题目
命题“x2-9=0的解是x=±3”,在这个命题中,使用的逻辑联结词的情况是( )
| A、没有使用逻辑联结词 |
| B、使用了“且” |
| C、使用了“或” |
| D、使用了“非” |
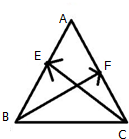 如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求
如图,在边长为2的正△ABC中,E、F分别是AB、AC的中点,求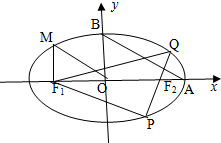 如图,从椭圆
如图,从椭圆