题目内容
已知f(x)为R上的奇函数,当x>0时.f(x)=x2-x.
(1)求f(x)的解析式;
(2)若f(x)=a恰有3个不同的解,求a的取值范围.
(1)求f(x)的解析式;
(2)若f(x)=a恰有3个不同的解,求a的取值范围.
考点:函数奇偶性的性质,函数解析式的求解及常用方法
专题:计算题,数形结合,函数的性质及应用
分析:(1)利用函数的奇偶性,利用对称性,写出函数y=f(x)的解析式;
(2)求出函数f(x)的表达式,利用数形结合的思想求a的取值范围;
(3)y=f(x)当x∈[1,2]时的图象恒在y=2x+2m+1的图象上方,x2-x>2x+2m+1在区间[1,2]恒成立,即2m<x2-3x-1在区间[1,2]恒成立,运用二次函数的对称轴和区间的关系,即可求得右边的最小值,令2m小于最小值即可.
(2)求出函数f(x)的表达式,利用数形结合的思想求a的取值范围;
(3)y=f(x)当x∈[1,2]时的图象恒在y=2x+2m+1的图象上方,x2-x>2x+2m+1在区间[1,2]恒成立,即2m<x2-3x-1在区间[1,2]恒成立,运用二次函数的对称轴和区间的关系,即可求得右边的最小值,令2m小于最小值即可.
解答:
 解:(1)当x∈(-∞,0)时,-x∈(0,+∞),
解:(1)当x∈(-∞,0)时,-x∈(0,+∞),
∵y=f(x)是奇函数,
∴f(x)=-f(-x)=-((-x)2-(-x))=-x2-x,且f(0)=0,
∴f(x)=
;
(2)当x∈[0,+∞)时,f(x)=x2-x=(x-
)2-
,最小值为-
;
∴当x∈(-∞,0)时,f(x)=-x2-x=
-(x+
)2,最大值为
.
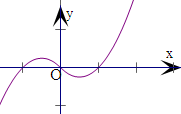
∴据此可作出函数y=f(x)的图象,根据图象得,
若方程f(x)=a恰有3个不同的解,则a的取值范围是(-
,
);
(3)∴在区间[1,2]内,y=f(x)=x2-x,
∵y=f(x)当x∈[1,2]时的图象恒在y=2x+2m+1的图象上方,
∴x2-x>2x+2m+1在区间[1,2]恒成立,即2m<x2-3x-1在区间[1,2]恒成立,
∵函数t=x2-3x-1在区间[1,
]是减函数,(
,2]上是增函数,
∴当x=
时,x2-3x-1的最小值是-
,
则2m<x2-3x-1在区间[1,2]恒成立,
可得,2m<-
,即m<-
.
 解:(1)当x∈(-∞,0)时,-x∈(0,+∞),
解:(1)当x∈(-∞,0)时,-x∈(0,+∞),∵y=f(x)是奇函数,
∴f(x)=-f(-x)=-((-x)2-(-x))=-x2-x,且f(0)=0,
∴f(x)=
|
(2)当x∈[0,+∞)时,f(x)=x2-x=(x-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴当x∈(-∞,0)时,f(x)=-x2-x=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴据此可作出函数y=f(x)的图象,根据图象得,
若方程f(x)=a恰有3个不同的解,则a的取值范围是(-
| 1 |
| 4 |
| 1 |
| 4 |
(3)∴在区间[1,2]内,y=f(x)=x2-x,
∵y=f(x)当x∈[1,2]时的图象恒在y=2x+2m+1的图象上方,
∴x2-x>2x+2m+1在区间[1,2]恒成立,即2m<x2-3x-1在区间[1,2]恒成立,
∵函数t=x2-3x-1在区间[1,
| 3 |
| 2 |
| 3 |
| 2 |
∴当x=
| 3 |
| 2 |
| 13 |
| 4 |
则2m<x2-3x-1在区间[1,2]恒成立,
可得,2m<-
| 13 |
| 4 |
| 13 |
| 8 |
点评:本题以二次函数为例,求函数在闭区间上的最值的表达式,并求不等式恒成立时参数的取值范围,着重考查了二次函数的单调性、图象的对称性和函数恒成立问题的讨论等知识,属于中档题.

练习册系列答案
相关题目