Question

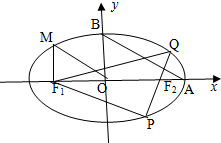如图，从椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）上一点M向x轴作垂线，恰好通过椭圆的左焦点F₁，且它的长轴端点A及短轴端点B的连线AB平行于OM，
（1）求椭圆的离心率；
（2）设Q是椭圆上任意一点，F₂是右焦点，求∠F₁QF₂的取值范围；
（3）设Q是椭圆上一点，当QF₂⊥AB时，延长QF₂与椭圆交于另一点P，若△F₁PQ的面积为4

3

，求此时的椭圆方程．

Answer 1

考点：直线与圆锥曲线的关系,椭圆的标准方程

专题：圆锥曲线的定义、性质与方程

分析：（1）通过求解F（-c，0），M(-c，

b2

a

)，利用AB∥OM，推出关系式，即可求解离心率．
（2）在△F₁QF₂中，利用余弦定理求出cos∠F₁QF₂=

2b2

a2

-1，推出cos∠F₁QF₂≥0，得到∠F₁QF₂的取值范围．
（3）由（1）知，b=c，设椭圆方程为

x2

2c2

+

y2

c2

=1，得到直线PQ的方程为y=

2

(x-c)，联立方程组

y= 2 (x-c) x2 2c2 + y2 c2 =1

，设Q（x₁，y₁），P（x₂，y₂），通过韦达定理得，利用写出公式求出QP，由点F₁到QP的距离，通过三角形的面积求出c²=5，得到椭圆方程．

解答： 解：（1）F（-c，0），M(-c，

b2

a

)，
因为AB∥OM，

b2 a

c

=

b

a

，得b=c，
则e=

c

a

=

2

2

．                      （2分）
（2）在三角形F₁QF₂中，由余弦定理得：cos∠F₁QF₂=

|QF1|2+|QF2|2-|F1F2|2

2|QF1||QF2 |

=

(|QF1|+|QF2|)2-2|QF1||QF2|-4c2

2|QF1||QF2|

=

2b2

|QF1||QF2|

-1≥

2b2

( |QF1|+|QF2| 2 )2

-1=

2b2

a2

-1，
又因为a²=2b²，所以cos∠F₁QF₂≥0，
即∠F1QF2∈[0，

π

2

]．           （5分） 
（3）由（1）知，b=c，故设椭圆方程为

x2

2c2

+

y2

c2

=1，kAB=-

2

2

，
因为QF₂⊥AB，所以kPQ=

2

，故直线PQ的方程为y=

2

(x-c)，（6分）
联立方程组

y= 2 (x-c) x2 2c2 + y2 c2 =1

，整理得5x²-8cx+2c²=0，记△=24c²＞0，
设Q（x₁，y₁），P（x₂，y₂），
由韦达定理得：x1+x2=

8c

5

，x1•x2=

2c2

5

，
|QP|=

(x2-x1)2+(y2-y1)2

=

1+( 2

)2•|x₂-x₁|=

6 2

5

c（8分）
又点F₁到QP的距离d=

2 6

3

c，
所以S=

1

2

•

6 2

5

c•

2 6

3

c=

4 3

5

c2=4

3

．
所以c²=5，故椭圆方程为

x2

10

+

y2

5

=1．（10分）

点评：本题考查直线与椭圆的位置关系的应用，三角形的面积的求法，弦长公式的应用，考查转化思想以及计算能力．