题目内容
6.已知函数y=3tan(2x-$\frac{π}{4}$)(1)求函数的最小正周期;
(2)求函数的定义域;
(3)说明此函数是由y=tanx的图象经过怎么样的变化得到的.
分析 (1)直接由正切型函数的周期公式求得周期;
(2)由相位的终边不在y轴上求得函数的定义域;
(3)直接结合函数图象的平移得答案.
解答 解:(1)由周期公式可得函数y=3tan(2x-$\frac{π}{4}$)的最小正周期为T=$\frac{π}{2}$;
(2)由$2x-\frac{π}{4}≠kπ+\frac{π}{2}$,得$x≠\frac{kπ}{2}+\frac{3π}{8},k∈Z$.
∴函数定义域为{x|$x≠\frac{kπ}{2}+\frac{3π}{8},k∈Z$};
(3)把y=tanx的图象先向右平移$\frac{π}{4}$个单位,得到y=tan(x-$\frac{π}{4}$),然后再把图象上点的横坐标缩小到原来的$\frac{1}{2}$,得到y=tan(2x-$\frac{π}{4}$),最后把所得图象点的纵坐标扩大到原来的3倍即可得到y=3tan(2x-$\frac{π}{4}$)的图象.
点评 本题考查正切型函数的图象变换和周期的求法,考查正切函数的定义域,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.直线ax+by=0与圆x2+y2+ax+by=0的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不能确定 |
15.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,过F2的直线与椭圆交于A、B两点,若△F1AB是以A为直角顶点的等腰直角三角形,则离心率为 ( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{5}$-2 | D. | $\sqrt{6}$-$\sqrt{3}$ |
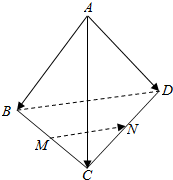 已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.
已知空间四边形ABCD,连接AC、BD,设M,N分别是BC,CD的中点,则$\overrightarrow{MN}$用$\overrightarrow{AB}$,$\overrightarrow{AC}$,$\overrightarrow{AD}$表示的结果为$\frac{1}{2}\overrightarrow{AD}$$-\frac{1}{2}\overrightarrow{AB}$.