题目内容
16．已知集合A={y|y=2x-1}，集合B={x|y=$\sqrt{{x}^{2}-4x+3}$}，全集U=R，则（∁UA）∩B为（ ）| A． | （-∞，1]∪[3，+∞） | B． | （-∞，-1） | C． | （3，+∞） | D． | （-∞，-1] |
分析 求出A中y的范围确定出A，求出B中x的范围确定出B，根据全集U=R求出A的补集，找出A补集与B的交集即可．
解答 解：由A中A={y|y=2x-1}=（-1，+∞），
∵全集U=R，
∴∁UA=（-∞，-1]，
由x2-4x+3≥0，即（x-1）（x-3）≥0，
解得：x≤1或x≥3，即B=（-∞，1]∪[2，+∞），
则（∁UA）∩B=（-∞，-1]，
故选：D．
点评 此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
5．已知复数$z=\frac{5a}{2+i}+\frac{1+i}{1-i}，a∈R$，若复数z对应的点在复平面内位于第四象限，则实数a的取值范围是（ ）
| A． | a＞1 | B． | a＜0 | C． | 0＜a＜1 | D． | a＜1 |
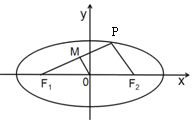已知P为椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上任意一点，F1，F2为左、右焦点，M为PF1中点．如图所示：若|OM|+$\frac{1}{2}$|PF1|=2，离心率e=$\frac{\sqrt{3}}{2}$．