题目内容
4．
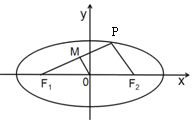已知P为椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上任意一点，F1，F2为左、右焦点，M为PF1中点．如图所示：若|OM|+$\frac{1}{2}$|PF1|=2，离心率e=$\frac{\sqrt{3}}{2}$．（1）求椭圆E的标准方程；
（2）已知直线l经过（-1，$\frac{1}{2}$）且斜率为$\frac{1}{2}$与椭圆交于A，B两点，求弦长|AB|的值．
分析 （Ⅰ）由|OM|+$\frac{1}{2}$|PF1|=2，又|OM|=$\frac{1}{2}$|PF2|，$\frac{1}{2}$|PF1|+$\frac{1}{2}$|PF2|=2，可得a．又e=$\frac{\sqrt{3}}{2}$=$\frac{c}{a}$，a2=b2+c2．解出即可得出．
（Ⅱ）法一：设直线l：y-$\frac{1}{2}$=$\frac{1}{2}$（x+1），联立直线与椭圆得：x2+2x=0，解出交点坐标利用两点之间的距离公式即可得出．
法二：联立方程得x2+2x=0，利用|AB|=$\sqrt{（1+\frac{1}{4}）[（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}]}$即可得出．
解答 解：（Ⅰ）由|OM|+$\frac{1}{2}$|PF1|=2，又|OM|=$\frac{1}{2}$|PF2|，∴$\frac{1}{2}$|PF1|+$\frac{1}{2}$|PF2|=2，
∴a=2．
离心率e=$\frac{\sqrt{3}}{2}$=$\frac{c}{a}$，a2=b2+c2．
解得b=1，c=$\sqrt{3}$．
故所求的椭圆方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1．
（Ⅱ）法一：设直线l：y-$\frac{1}{2}$=$\frac{1}{2}$（x+1），
联立直线与椭圆得：x2+2x=0，
所以，直线与椭圆相交两点坐标为（0，1），（-2，0）．
∴|AB|=$\sqrt{{1}^{2}+（-2）^{2}}$=$\sqrt{5}$．
法二：联立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=\frac{1}{2}x+1}\end{array}\right.$，得x2+2x=0，
∴x1+x2=-2，x1•x2=0，
∴|AB|=$\sqrt{（1+\frac{1}{4}）[（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{5}$．
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系、两点之间的距离公式、三角形中位线定理，考查了推理能力与计算能力，属于中档题．
提分百分百检测卷单元期末测试卷系列答案| A． | 3 | B． | -12 | C． | -3 | D． | 12 |
如图所示，在边长为2的正方形中有一封闭曲线围成的阴影区域．在正方形中随机撒一粒豆子，它落在阴影区域内的概率为$\frac{2}{3}$，则阴影区域的面积为$\frac{8}{3}$．| A． | （-∞，1]∪[3，+∞） | B． | （-∞，-1） | C． | （3，+∞） | D． | （-∞，-1] |
| A． | k=3 | B． | k=-3 | C． | k=$\frac{1}{3}$ | D． | k=-$\frac{1}{3}$ |