题目内容
若(x-
)8展开式中含x2的项的系数为7,则a=( )
| 1 |
| ax |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
考点:二项式系数的性质
专题:二项式定理
分析:利用二项展开式的通项公式求出第r+1项,令x的指数为2求出含x2的系数,列出方程解得.
解答:
解:(x-
)8展开式的通项为 Tr+1=
(x)8-r(-
)r=(-1)ra-r
x8-2r
令8-2r=2得r=3,
故展开式中x2项的系数为-a-3C85=7,解得a=-2,
故选:A.
| 1 |
| ax |
| C | r 8 |
| 1 |
| ax |
| C | r 8 |
令8-2r=2得r=3,
故展开式中x2项的系数为-a-3C85=7,解得a=-2,
故选:A.
点评:本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
向量
=(1,2),
=(1,-λ),在区间[-5,5]上随机取一个数λ,使向量2
+
与
-
的夹角为锐角的概率为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知复数z=3+4i,
表示复数z的共轭复数,则复数
在付平面内对应的点在( )
. |
| z |
| ||
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若条件p:(x-3)(x-4)=0,条件q:x-3=0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分条件也不必要条件 |
给出的图象中可能为函数f(x)=x4+ax3+cx2+bx+d(a,b,c,d∈R)的图象是( )
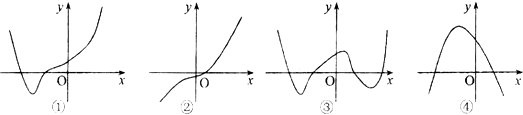

| A、①③ | B、①② | C、③④ | D、②④ |
执行如图所示的程序框图,输出的z值为( )


| A、7 | B、8 | C、9 | D、10 |