题目内容
在△ABC中，三个内角A、B、C成等差数列，则角A+C=（ ）
| A、30° | B、60° |
| C、90° | D、120° |
考点：等差数列
专题：等差数列与等比数列
分析：根据△ABC的内角和等于180°以及三个内角成等差数列，可以求出答案．
解答：
解：△ABC中，三个内角A、B、C成等差数列，
∴B=
（A+C）；
又∵A+B+C=180°，
∴A+C=120°．
故选：D．
∴B=
| 1 |
| 2 |
又∵A+B+C=180°，
∴A+C=120°．
故选：D．
点评：本题考查了等差数列的应用问题，解题时根据三角形的内角和定理与等差中项的公式，求出答案来，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
向量
=（1，2），
=（1，-λ），在区间[-5，5]上随机取一个数λ，使向量2
+
与
-
的夹角为锐角的概率为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若条件p：（x-3）（x-4）=0，条件q：x-3=0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分条件也不必要条件 |
若存在区间[m，n]，使得函数f（x）定义域为[m，n]时，其值域为[km，kn]（k∈N*），则称区间[m，n]为函数f（x）的“k倍区间”．已知函数f（x）=x3+sinx，则f（x）的“5倍区间”的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
给出的图象中可能为函数f（x）=x4+ax3+cx2+bx+d（a，b，c，d∈R）的图象是（ ）
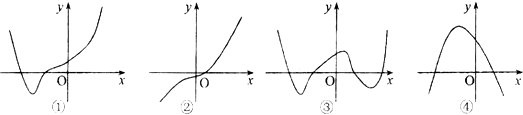
| A、①③ | B、①② | C、③④ | D、②④ |
若连续抛掷两次骰子得到的点数分别为m，n，m+n=5的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列表格提供了两个变量x与y之间的一组对应值，已知x，y间存在线性相关关系，且求得y关于x的线性回归直线方程为
=0.7x+0.35，那么表中t的值为（ ）
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.5 | 4 | t |
| A、3 | B、3.15 | C、3.5 | D、4 |
二项式（x2-
）n的展开式中各项系数的和为（ ）
| 1 |
| x |
| A、32 | B、-32 | C、0 | D、1 |