题目内容
等差数列{an}中，已知a1+a3=6，a5+a7=14，则a20+a22=（ ）
| A、44 | B、56 | C、42 | D、40 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：设出等差数列的公差，由题意列方程组求出首项和公差，再代入等差数列的通项公式得答案．
解答：
解：设等差数列{an}的公差为d，
由a1+a3=6，a5+a7=14，得：
，解得：
．
∴a20+a22=2a1+40d=2×2+40×1=44．
故选：A．
由a1+a3=6，a5+a7=14，得：
|
|
∴a20+a22=2a1+40d=2×2+40×1=44．
故选：A．
点评：本题考查了等差数列的通项公式，考查了等差数列的性质，是基础的计算题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
若条件p：（x-3）（x-4）=0，条件q：x-3=0，则p是q的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分条件也不必要条件 |
给出的图象中可能为函数f（x）=x4+ax3+cx2+bx+d（a，b，c，d∈R）的图象是（ ）
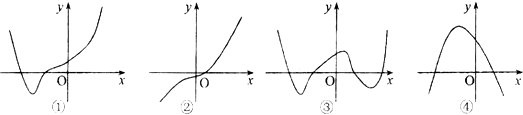
| A、①③ | B、①② | C、③④ | D、②④ |
若连续抛掷两次骰子得到的点数分别为m，n，m+n=5的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）=ax3+bx+2013，若f（2014）=4025，则f（-2014）的值为（ ）
| A、1 | B、-4025 |
| C、-2013 | D、2014 |
下列表格提供了两个变量x与y之间的一组对应值，已知x，y间存在线性相关关系，且求得y关于x的线性回归直线方程为
=0.7x+0.35，那么表中t的值为（ ）
 |
| y |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3.5 | 4 | t |
| A、3 | B、3.15 | C、3.5 | D、4 |
执行如图所示的程序框图，输出的z值为（ ）
| A、7 | B、8 | C、9 | D、10 |
为了了解调研高一年级新学生的智力水平，某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查，测得“智力评分”的频数分布表如表l，表2．