题目内容
某工厂有十批羊毛,在处理前后,分别测得含脂率(%)分别如下:
(1)将处理前后的羊毛含脂率用茎叶图表示,并由图出发分析比较后,你有何结论;
(2)若分别在处理前与处理后从这十批羊毛中各随机抽出1批羊毛进行检查,求两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率;
(3)为了检查羊毛抽脂机的抽脂性能,请设计一程序框图,求出羊毛处理前的含脂率x%关于处理后的含脂率y%的线性回归方程
=bx+a中的斜率b与截距a.
(计算公式)b=
,a=
-b
.
| 羊毛一 | 羊毛二 | 羊毛三 | 羊毛四 | 羊毛五 | 羊毛六 | 羊毛七 | 羊毛八 | 羊毛九 | 羊毛十 | |
| 处理 前x | 6 | 14 | 15 | 20 | 21 | 23 | 30 | 33 | 44 | 56 |
| 处理 后y | 4 | 5 | 7 | 8 | 10 | 12 | 13 | 15 | 16 | 26 |
(2)若分别在处理前与处理后从这十批羊毛中各随机抽出1批羊毛进行检查,求两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率;
(3)为了检查羊毛抽脂机的抽脂性能,请设计一程序框图,求出羊毛处理前的含脂率x%关于处理后的含脂率y%的线性回归方程
 |
| y |
(计算公式)b=
| |||||||
|
. |
| y |
. |
| x |
考点:线性回归方程
专题:综合题,概率与统计
分析:(1)根据所给数据,可得茎叶图表示,并由图出发分析比较后,可得结论;
(2)求出处理前和处理后都没有抽到含脂率在5%到15%之间(包括5%与15%)的羊毛的可能结果有7×3=21种,利用间接法求出两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率;
(3)利用算法,可得程序框图.
(2)求出处理前和处理后都没有抽到含脂率在5%到15%之间(包括5%与15%)的羊毛的可能结果有7×3=21种,利用间接法求出两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率;
(3)利用算法,可得程序框图.
解答:
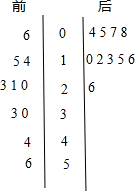 解:(1)茎叶图如图所示:
解:(1)茎叶图如图所示:
结论:从图中可以看到处理前羊毛含脂率分布范围广,平均含脂率较高,处理后羊毛含脂率下降,而且含脂率取值波动较小.(说明:按照平均数、众数、中位数、方差这几个量的说明酌情给分)
(2)处理前和处理后都没有抽到含脂率在5%到15%之间(包括5%与15%)的羊毛的可能结果有7×3=21种,所以两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率为P=1-
=
,
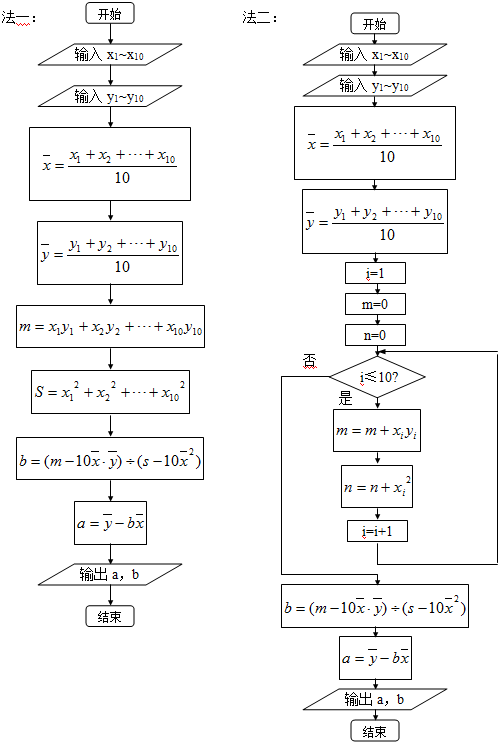
(3)如图所示:
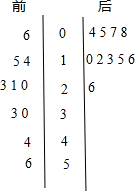 解:(1)茎叶图如图所示:
解:(1)茎叶图如图所示:结论:从图中可以看到处理前羊毛含脂率分布范围广,平均含脂率较高,处理后羊毛含脂率下降,而且含脂率取值波动较小.(说明:按照平均数、众数、中位数、方差这几个量的说明酌情给分)
(2)处理前和处理后都没有抽到含脂率在5%到15%之间(包括5%与15%)的羊毛的可能结果有7×3=21种,所以两次检查中至少有1批羊毛含脂率在5%到15%之间(包括5%与15%)的概率为P=1-
| 21 |
| 100 |
| 79 |
| 100 |
(3)如图所示:

点评:本题考查统计知识,考查算法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

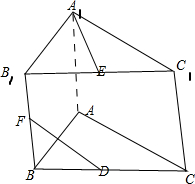 如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.
如图,在三棱柱ABC-A1B1C1中,AB=AC,侧棱AA1垂直于底面,D、E分别为BC、B1C1的中点,F为侧棱BB1上的一点.