题目内容
 如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程.
如图示,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于C,若|BC|=2|BF|,且|AC|=5,求此抛物线的方程.考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),由直线l交抛物线准线于点C,|BC|=2|BF|,可得x2=
,|BC|=2|BF|,且|AC|=5,可得x1=5-
,利用抛物线的性质x1x2═
,建立关于p的方程,解之可得p,即得此抛物线的方程.
| p |
| 6 |
| 5p |
| 2 |
| p2 |
| 4 |
解答:
解:设A(x1,y1),B(x2,y2)
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
,
由抛物线的定义,得|AF|=
+x1,
∵|BC|=2|BF|,且|AC|=5,
∴
+x1+3(
+x2)=5
∴x1=5-
,
由抛物线的性质,得x1x2=(5-
)•
=
,
解之得p=
,可得此抛物线的方程为y2=
x.
∵直线l交抛物线准线于点C,|BC|=2|BF|,
∴x2=
| p |
| 6 |
由抛物线的定义,得|AF|=
| p |
| 2 |
∵|BC|=2|BF|,且|AC|=5,
∴
| p |
| 2 |
| p |
| 2 |
∴x1=5-
| 5p |
| 2 |
由抛物线的性质,得x1x2=(5-
| 5p |
| 2 |
| p |
| 6 |
| p2 |
| 4 |
解之得p=
| 5 |
| 4 |
| 5 |
| 2 |
点评:本题给出抛物线满足的条件,求抛物线的方程.着重考查了抛物线的定义与标准方程、直线与圆锥曲线位置关系等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
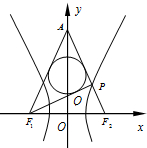 如图,已知双曲线
如图,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
| A、3 | ||
| B、2 | ||
C、
| ||
D、
|
已知l,m是两条不同的直线,α是一个平面,且l∥α,则下列命题正确的是( )
| A、若l∥m,则m∥α |
| B、若m∥α,则l∥m |
| C、若l⊥m,则m⊥α |
| D、若m⊥α,则l⊥m |
 如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为
如图所示,在边长为1的正方形OABC中任取一点M,则点M恰好取自阴影部分的概率为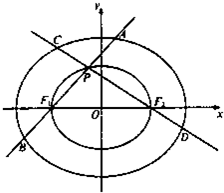 已知椭圆
已知椭圆