题目内容
如图所示，在边长为1的正方形OABC中任取一点M，则点M恰好取自阴影部分的概率为考点：几何概型,定积分在求面积中的应用
专题：概率与统计
分析：欲求所投的点落在阴影部分内部的概率，须结合定积分计算阴影部分平面区域的面积，再根据几何概型概率计算公式易求解．
解答：
解：由题意可知，此题求解的概率类型为关于面积的几何概型，
由图可知基本事件空间所对应的几何度量S（Ω）=1，
曲线y=x2与x轴，x=1所围成的图形的面积S，即满足所取的点落在阴影部分内部所对应的几何度量：
S（A）=
x2dx=（
x3）
=
．
则点M取自阴影部分的概率为P（A）=
．
故答案为：
．
由图可知基本事件空间所对应的几何度量S（Ω）=1，
曲线y=x2与x轴，x=1所围成的图形的面积S，即满足所取的点落在阴影部分内部所对应的几何度量：
S（A）=
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
则点M取自阴影部分的概率为P（A）=
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查了利用定积分求面积以及几何摡型知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
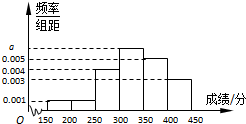某地区教育主管部门为了对该地区模拟考试成绩进行分析，随机抽取了150分到450分之间的1000名学生的成绩，并根据这1000名学生的成绩画出样本的频率分布直方图（如图），则成绩在[300，350）内的学生人数共有设集合U={x∈N*|x≤4}，A={1，2}，B={2，4}，则（∁UA）∪B=（ ）
| A、{1，2} |
| B、{1，2，3，4} |
| C、{3，4} |
| D、{2，3，4} |
若按如图的算法流程图运行后，输出的结果是
，则输入的N的值为（ ）
| 6 |
| 7 |
| A、5 | B、6 | C、7 | D、8 |
如图示，过抛物线y2=2px（p＞0）的焦点F的直线l交抛物线于点A，B，交其准线于C，若|BC|=2|BF|，且|AC|=5，求此抛物线的方程．