题目内容
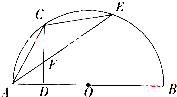如图，半圆O的直径AB的长为4，点C平分弧AE，过C作AB的垂线交AB于D，交AE干F．（Ⅰ）求证：CE2=AE•AF：
（Ⅱ）若AE是∠CAB的角平分线，求CD的长．
考点：相似三角形的判定,相似三角形的性质
专题：立体几何
分析：（I）利用点C平分
，可得
=
，CE=CA，∠CAE=∠CEA=∠FCA，进而得到△AFC∽△ECA．即可得出．
（II）由AE平分∠CAB，可得∠BAE=∠EAC=∠CEA，可得CE∥AB，于是∠ECD=90°，∠CAB=60°，即可得出．
 |
| AE |
|
| CE |
|
| CA |
（II）由AE平分∠CAB，可得∠BAE=∠EAC=∠CEA，可得CE∥AB，于是∠ECD=90°，∠CAB=60°，即可得出．
解答：
（I）证明：∵点C平分
，∴
=
，∴CE=CA，
∴∠CAE=∠CEA=∠FCA，
∴△AFC∽△ECA．
∴
=
，
∴CE2=AE•AF．
（II）解：∵AE平分∠CAB，∴∠BAE=∠EAC=∠CEA，
∴CE∥AB，
∴∠ECD=90°，∠BAE=∠EAC=∠CEA=30°，
∴∠CAB=60°，
∴CD=2sin60°=
．
|
| AE |
|
| CE |
|
| CA |
∴∠CAE=∠CEA=∠FCA，
∴△AFC∽△ECA．
∴
| AF |
| EC |
| AC |
| EA |
∴CE2=AE•AF．
（II）解：∵AE平分∠CAB，∴∠BAE=∠EAC=∠CEA，
∴CE∥AB，
∴∠ECD=90°，∠BAE=∠EAC=∠CEA=30°，
∴∠CAB=60°，
∴CD=2sin60°=
| 3 |
点评：本题考查了圆的性质、相似三角形的判定与性质、等边三角形的性质、直角三角形的边角关系，考查了推理能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
某高校在2012年的自主招生考试中随机抽取60名学生的笔试成绩，按成绩共分成五组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100），得到的频率分布直方图如图所示，同时规定成绩在85分以上（含85分）的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．
如图，已知∠A=60°，P、Q分别是∠A两边上的动点．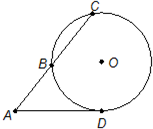
如图，从圆O外一点A引圆的切线AD和割线ABC，已知AD=4